本篇博客仅作为学习,如有侵权必删。
1. 信息量:
一个事件发生的概率越小,信息量越大,所以信息量应该为概率的减函数,对于相互独立的两个事有p(xy)=p(x)p(y),对于这两个事件信息量应满足h(xy)=h(x)+h(y),那么信息量应为对数函数:
h(x) = -ln p(x)
对于一个随机变量可以以不同的概率发生,那么通过信息量期望的方式衡量,即信息熵。
2. 熵
熵:信息不确定性度量(信息量与不确定性相关)。事件发生的概率越小则携带的信息越大。
一个离散随机变量X的可能取值为X=x1,x2,…,xn,而对应的概率为pi=p(X=xi),则随机变量的熵定义为:
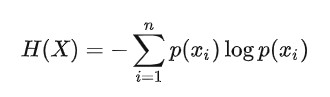
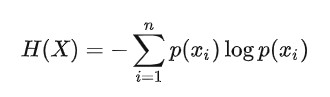
每个xi表示一种特征。 H(X)在每个p(xi) = 1/N是最大,N为信息的个数。在概率为1/N时信息是最不确定的。
规定当p(xi)=0时,p(xi)log(p(xi)=0
【小思考:为何公式是这样子的?其实只需熵和概率P成反比,1/P , 但是有个量纲缺点:地震发生的概率很小(P = 1/百万),则信息量为一百万。抛硬币概率1/2,则信息量为2。两者量纲差太大,取log之后,使得低范围的值稍微放大,高范围的值稍微放小。】
3. 联合熵H(p,q)
两个随机变量的p与q的联合分布形成的熵称为联合熵,记为H(p, q)。
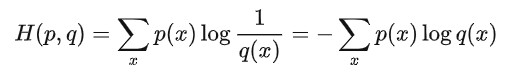
4. 条件熵H(q|p)
X给定的条件下,Y的信息熵,即H (Y |X )。公式为:
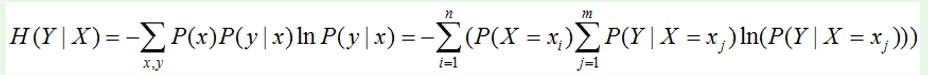
推导过程:
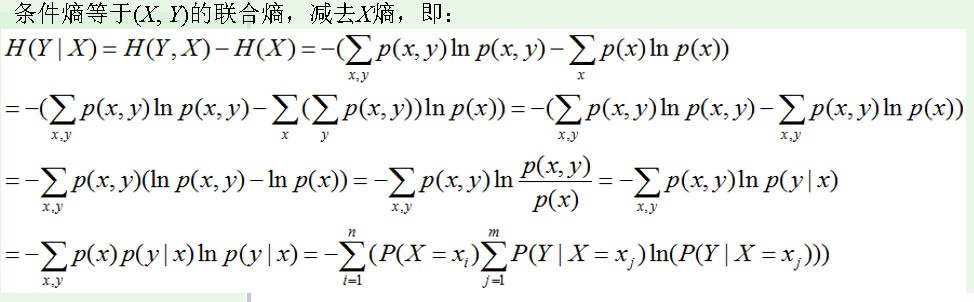
5. KL散度(相对熵):
交叉熵:两个概率分布之间的一个比较,如果两个分布越匹配,交叉熵就越低;如果两个概率分布完全比配,那么交叉熵就为 0。
如果是两个随机变量P,Q,且其概率分布分别为p(x),q(x),则p相对q的相对熵为:
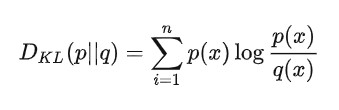
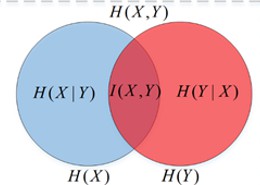
6. 几种熵之间的关系: