本篇博客仅作为学习,如有侵权必删。
正则化/惩罚项
一、概念
(1)范数:
(2)方差和偏差:
Error = Bias + Variance
- Error反映的是整个模型的准确度,
- Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,
- Variance反映的是模型每一次输出结果与模型输出期望之间的误差(描述的是样本上训练的模型在测试集上的表现。),即模型的稳定性。
- 欠拟合是高bias,过拟合是高variance。
(3)正则化的目的:减少模型参数大小或者参数数量,缓解过拟合。
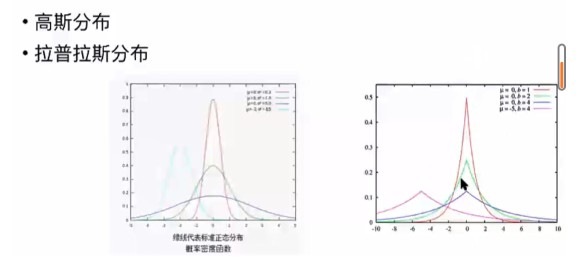
正则化的作用是给模型加一个先验,lasso(l1)认为模型是拉普拉斯分布,ridge(l2)认为是高斯分布,正则项对应参数的协方差,协方差越小,这个模型的variance越小,泛化 能力越强,也就抵抗了过拟合。
(4)正则化通用形式:
Loss_with_regularization = loss(w,x) + λf(w)
- 正则化恒为非负
- f(w)不能为负数,若其为负数,Loss(w,x)+λf(x)本来尽可能想让其变小,那f(x)为负数,f(x)绝对值会越学越大。
(5) 正则化方法:L1正则、L2正则、Dropout正则
二、 从数学角度解释正则化为什么能提升模型的泛化能力;【奥卡姆剃刀:简单就好】
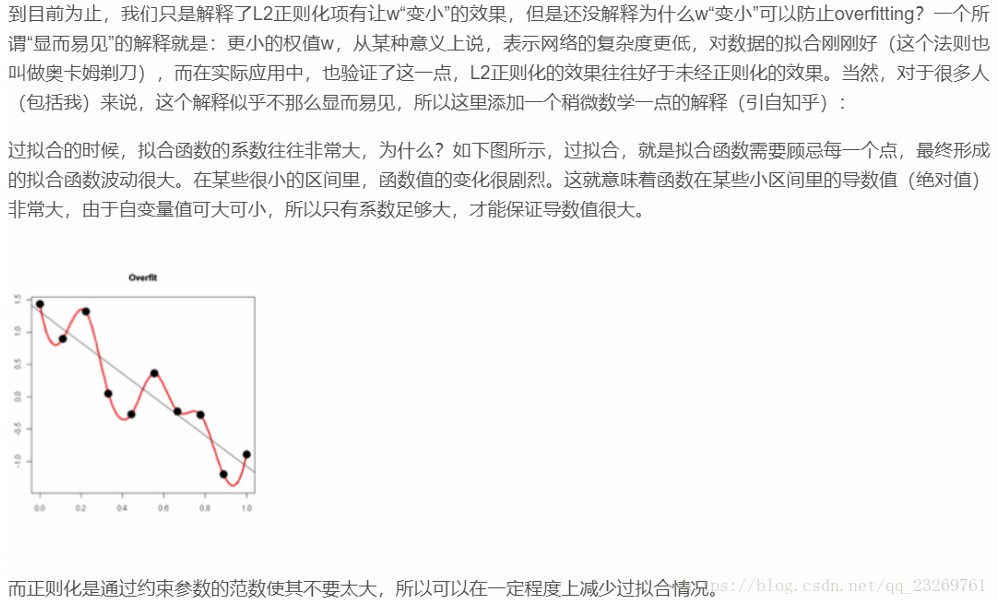
过拟合就是模型在学习训练样本时将噪声异常值也学习得非常好,使得模型参数过多,模型较复杂,给参数加上一个先验约束,可降低过拟合。
三、L1和L2范数各有什么特点以及相应的原因?L1和L2的区别与应用场景;
区别:L1假设参数服从拉普拉斯分布,L2则符合高斯分布;
L1范数更容易产生稀疏的权重,L2范数更容易产生分散的权重。
原因:(L1稀疏的原因,L2不稀疏的原因)【几何、公式两个角度】
场景:具有高维的数据特征时采用L1正则效果好一点。因为L1具有稀疏性。
四、解释L1范数更容易产生稀疏的权重,L2不的原因:
(1)几何角度
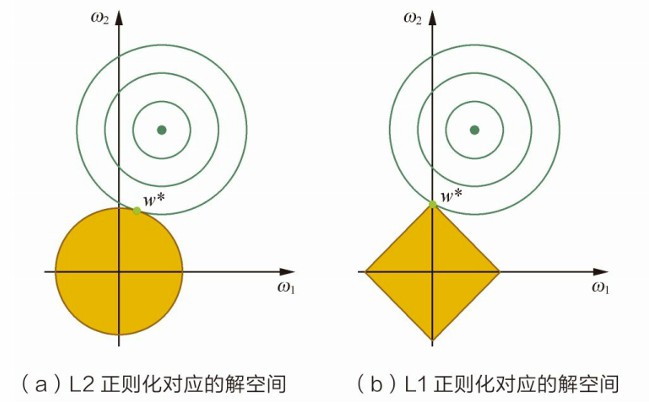
L2正则项约束后的解空间是圆形,L1正则项约束后的解空间是多方形,L1易在角点发生交点,从而产生稀疏解。
绿色等高线代表未施加正则化的代价函数,菱形和圆形分别代表L1和L2正则化约束,L1-ball 与L2-ball的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,而目标函数的”等高线”除非位置摆得非常好,大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性。相比之下,L2-ball 就没有这样的性质,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小
(2)公式角度:(拉格朗日求导)
深度学习花书7.1节(202页左右)。带L1正则化的最优参数w=sign(w) max{|w|- a/H , 0},其中w代表未正则化的目标函数的最优参数,H代表海森矩阵,a是正则化系数,只要a足够大,w就会在更大区间范围内使w变为0,而带L2正则化的最优参数w=H/(H+a)▪w,只要w不为0,w也不为0.
1、稀疏性的约束:
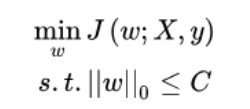
L1范数和L0范数可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用。
2、不好求解,松弛为L1,L2:
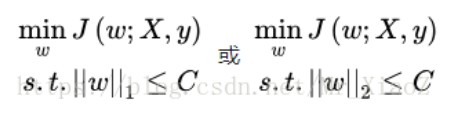
3、拉格朗日

(3)贝叶斯先验
L1正则化相当于对模型参数w引入了拉普拉斯先验,L2正则化相当于引入了高斯先验,而拉普拉斯先验使参数为0的可能性更大。
L1正则化可通过假设权重w的先验分布为拉普拉斯分布,由最大后验概率估计导出。
L2正则化可通过假设权重w的先验分布为高斯分布,由最大后验概率估计导出。
详细解释: https://blog.csdn.net/m0_38045485/article/details/82147817