本篇博客仅作为学习,如有侵权必删。
[TOC]
梯度下降
1. 重点
(1) 常用的优化方法:牛顿法、GD、拟牛顿法、共轭梯度法,之间的区别
(2) GD三种变形:BGD、SGD、MBGD
(3) 多种改进方法:Momentum、NAG、Adagrad、Adadelta、RMSProp、Adam
2. 概念
(1)常用的优化方法:直接法、迭代法(梯度下降、牛顿法、拟牛顿法、共轭梯度法)
(2)直接法(求解析解):
求梯度,令梯度为0
(3)牛顿法:

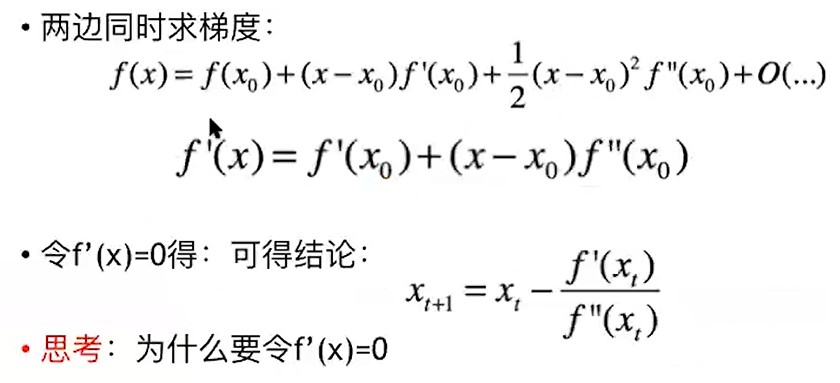
(4) GD 梯度下降:
让变量沿着目标函数负梯度的方向移动,直到移动到极小值点。
从拉格朗日中值定理 / 泰勒展开一阶公式都可以推出损失函数下降最大的方向是梯度方向。


3. 梯度下降法和牛顿法的区别
牛顿法和梯度下降法对比:
- 从公式上看,牛顿法是二阶收敛,梯度下降是一阶收敛(局部最优),所以牛顿法就更快。
【如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。】
- 从几何上看,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
4. 三种变形
GD的三种变形:BGD、SGD、MBGD
这三种形式的区别就是取决于我们用多少数据来计算目标函数的梯度。
(1)Batch gradient descend【批量梯度下降】
定义:【采用整个训练数据集的数据计算损失函数对参数的梯度】
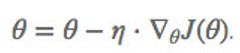
优点:全局最优解;易于并行实现;
- 缺点:大样本数据计算速度非常慢,不能投入新数据实时更新模型。
- 收敛:对于凸函数可以收敛到全局最优,对于非凸函数可以收敛到局部最优。
(2) Stochastic gradient descent【随机梯度下降】【适合在线更新】
- 定义:SGD 每次更新时对一个样本进行梯度更新。
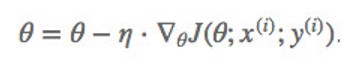
- 优点:对于很大的数据集来说,可能会有相似的样本,这样 BGD在计算梯度时会出现冗余, 而 SGD 一次只进行一次更新,就没有冗余,而且比较快,并且可以新增样本。
- 缺点:但是 SGD 因为更新比较频繁,会造成 cost function 有严重的震荡。准确度下降,不易于并行实现。
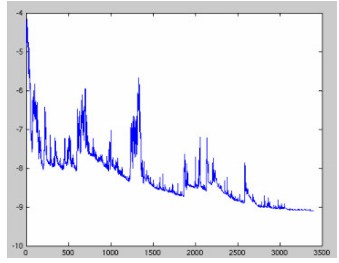
- 收敛性:不一定每次更新朝着最优值方向,因为存在噪音点,局部最优。
(3)mini-batch GD【小批量梯度下降】:降低随机梯度的方差
【在更新每一参数时都使用一部分样本来进行更新】
 ‘
‘
- 缺点:需要指定batch大小,收敛性不好。
- 一般batch取2的幂次能充分利用矩阵运算操作(32,64,128……)

三种方法的使用情况:
如果样本量比较小,采用批量梯度下降算法。如果样本太大,或者在线算法,使用随机梯度下降算法。在实际的一般情况下,采用小批量梯度下降算法。
GD具有的几个问题:
1、学习率选择【太小,收敛速度慢,太大,在最优值附近震荡】
2、学习率不固定【稀疏数据,学习率可增大】
3、(尤其SGD)对于非凸函数,易陷于局部最优值/鞍点。
5、优化方法
(1)动量Momentum【一般为SGD+momentum】
原理:因为SGD易陷于局部最优点或鞍点,一种帮助SGD在相关方向进行加速并抑制振荡的方法
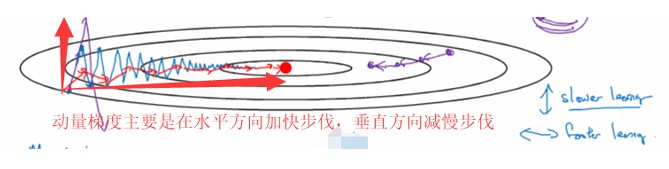

momentum表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,一般改为0.9。
α是学习率,即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。
- 优点:因此获得了更快的收敛性和减少了震荡。
- 缺点:这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚,如果它能具备一些先知,例如快要上坡时,就知道需要减速了的话,适应性会更好。