广告校准

发表于 | 分类于 ，

本篇博客仅作为学习,如有侵权必删。

https://zhuanlan.zhihu.com/p/460061332

https://zhuanlan.zhihu.com/p/582530785

https://zhuanlan.zhihu.com/p/398235467

广告校准

1. 业务背景

广告三大角色：广告主、媒体、DSP

  1. ctr : (Click Through Rate) 点击率 = click / show， 曝光广告中用户点击的概率。
  2. cvr: (Conversion Rate) 转化率 = order / click，点击广告中用户转化的概率。（如注册，激活，创角等）
  3. cpa：(Cost per Action) 转化成本 = cost / order, 表示广告主每获得一个转化需付的成本。
  4. ecpm / rpm：= ctr cvr cpa
    1. ecpm : 对广告主来说，(Effective Cost Per Mile) 每千次展示的有效费用。
    2. rpm：对DSP来说，(Revenue Per Mile)每千次展示的收入。
  5. pctr: (Predict CTR) 预估点击率
  6. pcvr: (Predict CVR) 预估转化率

2. 面临的问题

（1）模型准确性存在偏差，受限于

​ 实际分布和离线分布的差异

​ 模型学习能力

（2）预估模型的准确性度量

​ AUC：仅作为排序指标，无法度量预估值的大小准确性

​ COPC：（Click On Predict Click) = sum( 实际ctr) / sum(pctr)

​ 用于评估某段细分的流量模型预估值是否偏差较大。

（3）校准评价指标：

​ PCOC：（predict click over click）COPC是相反的指标。

​ cal-N：（calibration-N）

​ cal-N将样本集合分桶后分别计算PCOC，并计算与1的偏差作为标准误差。举个例子，将pctr根据值大小划分为多个桶，每个桶为一个簇，计算每个簇的PCOC及其与1的偏差 数学公式:

​ GC-N：（grouped calibration-N）

​ 在具体业务场景下，有时会重点关注某一维度下的校准效果(如广告计费维度)，GC-N可以解决这个问题，它可以在cal-N基础上自定义各维度权重。例如，下面这个式子定义了m个广告计划的GC-N 数学公式:

3. 校准算法

img

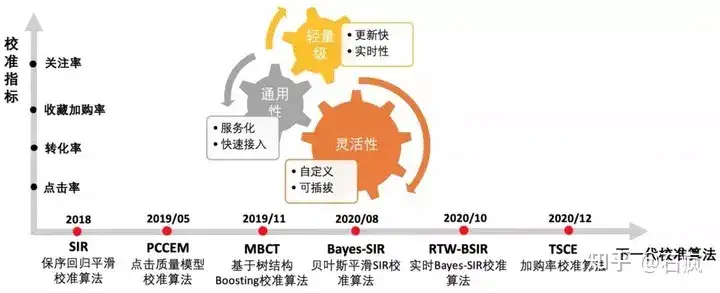
（1） Bias Correction：负采样率修正

原因：正负样本不均衡情况下，负采样通常可以提升模型的AUC精度，但pctr值会发生变化，与真实差距扩大。

校准公式：

因此可以计算出校准后的bias: b′=b+log(n)

代码：

注意在导出模型时，最终结果过完sigmoid，再进行bias_correct。

1
2
3
4
5
6
7
8
9
10
11
12
13
import math
def bias_correct(b, nr):
	"""
	nr: neg_sample_rate
	
	"""
    if nr < 1:
        return b + math.log(nr)
    else:
        return b

nr = 0.1 # 负采样率
last_op['bias'] = bias_correct(last_op['bias']， nr) # 纠正sigmoid后的bias

（2）校准算法—保序回归

解决模型高低估、模型over-confidence等问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def get_sir_calibration_model(pctr_list = [0.01,0.02,0.03,0.04], ctr_list = [0,1,0,1], bin_size = 0.01):
	sort_ctr_list = sorted(list(zip(pctr_list, ctr_list)), key = lambda x:x[0])
    bin_index = 0
    ind = 0
    n = len(ctr_list)
    cctr_res = []
    while ind < n:
        while (bin_index + bin_size) < sort_ctr_list[ind][0]:
            cctr_res.append(sort_ctr_list[ind][1])
            bin_index += 1
        if (bin_index + bin_size) == sort_ctr_list[ind][0]:
            cctr_res.append(sort_ctr_list[ind][1])
            ind += 1
            bin_index += bin_size
            continue
        if ind + 1== n:
            break
        tmp_cctr = sort_ctr_list[ind + 1][1]
        tmp_num = 1
        while ind + 1 < n and bin_index + bin_size > sort_ctr_list[ind][0]:
            tmp_cctr += sort_ctr_list[ind][1]
            tmp_num += 1
            ind += 1
        cctr_res.append(tmp_cctr/tmp_num)
        bin_index += bin_size

（3）校准算法3 —-SIR（保序回归平滑校准算法）

解决桶间数据稀疏问题

SIR算法是18年提出的，如上图所示，结合了Binning、Isotonic Regression和线性Scaling方法。

具体思想为：

  1. 进行保序回归。

  2. 使用单调平滑函数拟合模型预估值和实际点击率的映射关系（线性Scaling）就得到了校准函数。

该算法的优势在于充分利用了保序和平滑思想缓解了数据稀疏的问题。

（详细可见论文：Calibrating user response predictions in online advertising）。

（4）校准算法4—贝叶斯平滑SIR校准算法（Bayes-SIR)

  • Bayes-SIR解决冷启动问题。

  • beta分布：可以看作一个概率的概率分布

    带你理解beta分布

  • 贝叶斯平滑方法:（最早在雅虎的一篇论文里面中提出，用于解决数据稀疏问题下的点击率预估优化）。

在SIR算法应用中，发现广告计划投放初期校准效果明显差于平均水平，并在实际业务中造成以下问题：

1）影响新建计划初始阶段的投放表现；

2）影响强时效性广告的全生命周期效果；

3）小客户在整个投放周期里数据一直稀疏，得不到准确的校准，影响竞价公平性。

这是SIR校准算法的冷启动问题，采用了Bayes平滑的思想进行优化.

Bayes-SIR的算法思想：如上图所示，

  1. 从丰富的先验数据中估计出每个广告计划的点击率先验分布，

  2. 依据该先验知识求解出belta分布的参数α和β。

  3. 依据α和β和新观测到的少量数据，计算得到更准确的后验点击率。

这种估计方法能充分利用先验知识，具备置信程度过渡平滑的特点。

将贝叶斯平滑CTR估计过程替换掉SIR算法的朴素CTR统计逻辑即构成了具有冷启动问题优化效果的校准方法。

实际上线后，新广告的投放效果得到明显的提升。