RDD

发表于 2023-03-11 | 分类于大数据， Spark

本文仅做学习总结，如有侵权立删

[TOC]

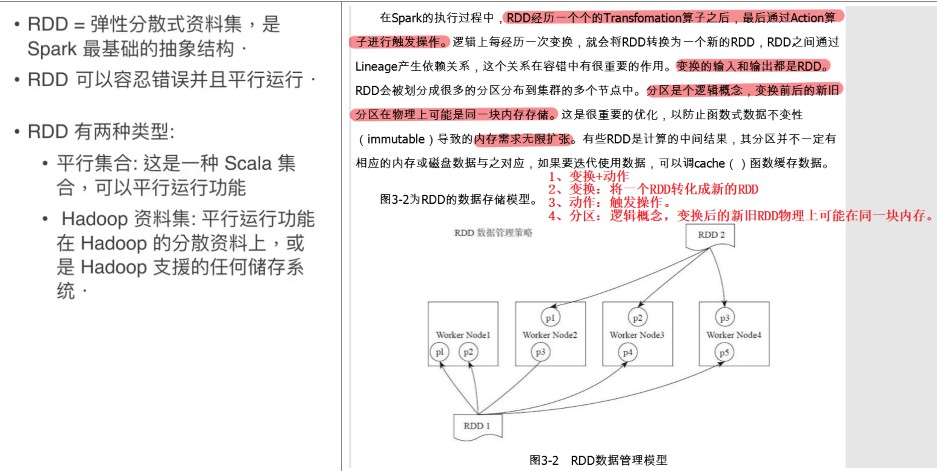
一、理解RDD

RDD可以被抽象地理解为一个大的数组，但是这个数组是分布在集群上的。

二、RDD的生命周期

创建—变换—动作（结束）

三、RDD依赖

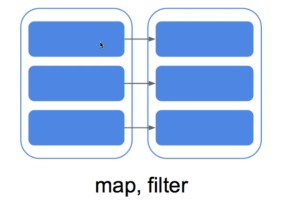
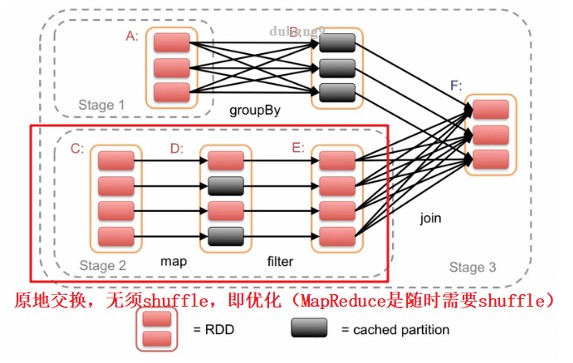
1、窄依赖（RDD）—–原地变换，不需要shuffle【即各个RDD之间不需要统计】

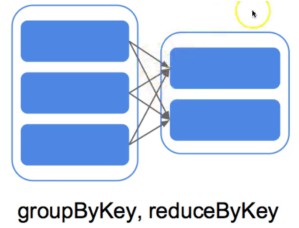
2、宽依赖（RDD）—–需要shuffle，与其他RDD交换资料，时间消耗长。

3、任务优化，如

四、RDD的基本操作

RDD可以有两种计算操作算子：Transformation（变换）与Action（行动）。

1、基本的RDD

（1）建立RDD

1 2	wordsList = ['cat','ele','rat','rat','cat'] wordsRDD = sc.parallelize(wordsList , 4)

#建立RDD wordsList = ['cat','ele','rat','rat','cat'] wordsRDD = sc.parallelize(wordsList , 4)

#计算法每个单词的长度 wordsRDD.map(len).collect()

（2）转换操作

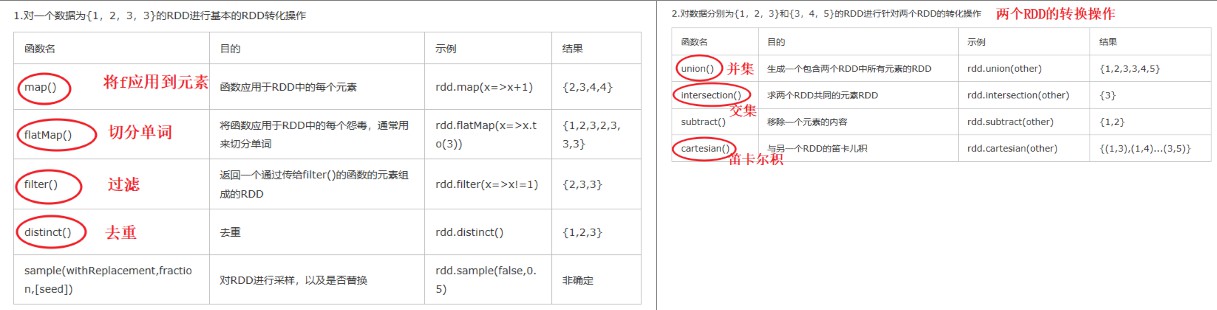
（3）动作操作

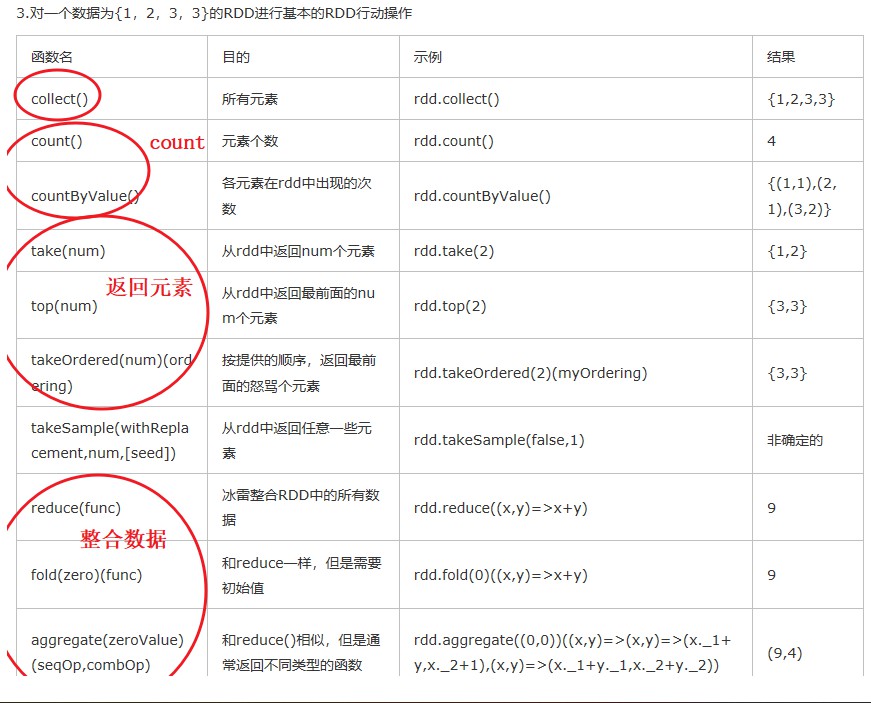
（4）通过pipe方法调用系统命令操作RDD

每个输入分区的所有元素被当做另一个外部进程的标准输入，输入元素由换行符分隔。

最终结果由该外部进程的标准输出生成，标准输出的每一行产生输出分区的一个元素。

例子：将每个分区传递给wc命令。每个元素将作为一个输入行，因此执行行计数，将得到每个分区的总行数：

1 2	words.pipe("wc -l").collect() # 结果显示:每个分区有5行。

（5）mapPartitions：每次处理一个分区

Spark 在实际执行代码时是基于每个分区运行的，所有map函数只是mapPartitions基于行操作的一个别名，

mapPartitions函数每次处理一个数据分区（可以通过迭代器来遍历该数据分区），不是具体的一行。

例子：为数据中的每个分区创建值“1”，以下表达式中计算总和将得出我们拥有的分区数量：

1	words.mapPartitions(lambda part:[1]).sum() #2

应用场景：将属于某类的值收集到一个分区中，然后对整个分组进行操作。

（6）mapPartitionsWithIndex：接收两个参数，一个位分区的索引和另一个为遍历分区内所有项的迭代器。

mapPartitionsWithIndex应用场景：测试map函数是否正确运行。

1
2
3

def indexedFunc(partitionIndex, withinPartIterator):
	return ["partition:{} => {}".format(partitionIndex, x) for x in withinPartIterator]
words.mapPartitionsWithIndex(indexedFunc).collect()

（7）foreachPartition：与mapPartitions函数类似，但不需要返回值

mapPartitions函数需要返回值才能正常执行，但foreachPartition函数不需要。

foreachPartition函数仅用于迭代所有的数据分区，与mapPartitions的不同在于它没有返回值，适合写入数据库操作（不需要返回计算结果）。

（8）glom: 将每个分区都转换为数组。

当需要将数据收集到驱动器并想为每个分区创建一个数组时，就很适合用glom函数实现。但会导致严重的稳定性问题，当有很大的分区或大量分区时，该函数会导致驱动器崩溃。

1 2	spark.sparkContext.parallelize(["hello" , "words"], 2).glom().collect() # 结果是[["hello", "worlds"]]

2. 键值对PairRDD：算子中包含ByKey的都是针对PairRDD

（1）创建PairRDD

是一种以（key,value)方式存储的RDD。

pairRDD = wordsRDD.map(lambda x : (x , 1))

keyBy：根据当前value创建key的函数。

1 2	# 将单词中的第一个字母作为key, 然后Spark将该单词记录保存为RDD的value keyword = words.keyBy(lambda word: word.lower()[0])

(2) 转换操作

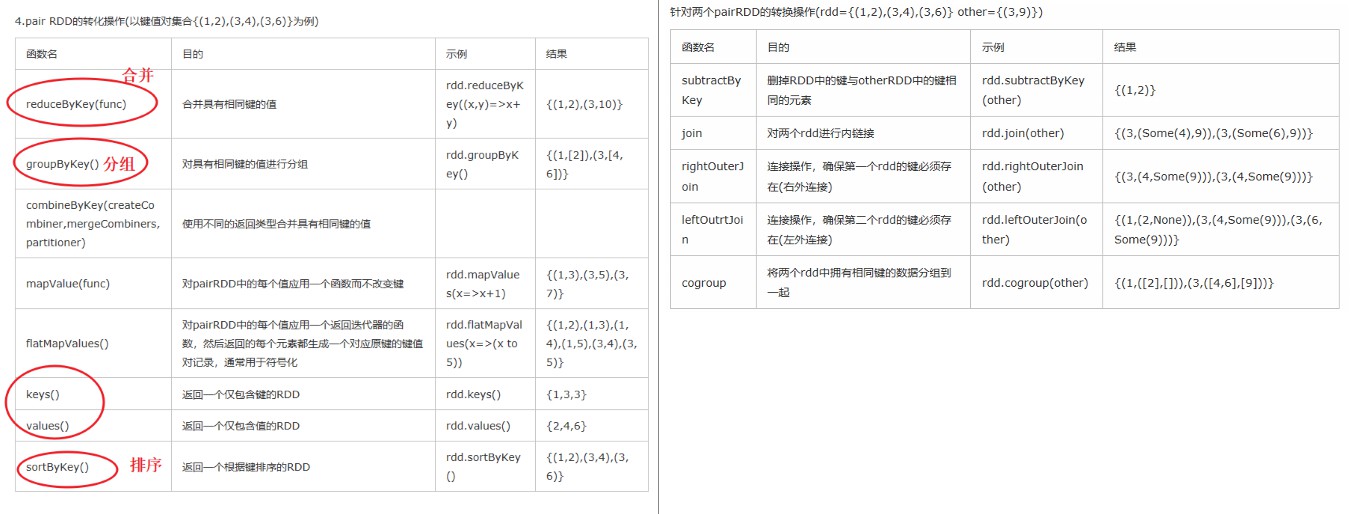
mapValue：只修改value，不修改key

Keyword.mapValues(lambda word:word.upper()).collect()
# 结果：
'''
[('s', 'SPARK'),
('t'),'THE']
'''

flatMapValues：在row（行）上进行flatMap操作来扩展行数
keys() / values()：提取keys或value
sampleByKey：通过一个key来采样RDD

(3) 动作操作

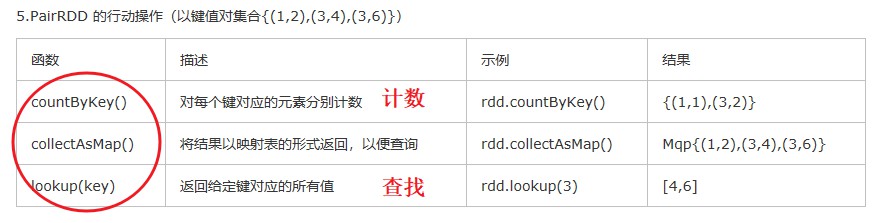
lookup：查找某个key对应的value, 因为同一个key可能有多个value，例子：查找’s’时，将获得与该key相关的两个value, 即’Spark’和’Simple’

1	keyword.lookup("s")

一些小问题：

1、spark中的RDD是什么

概念：分布式数据集，**spark**中基本的数据抽象，代表一个不可变、可分区、元素可并行计算的集合。

2、RDD的五大特性：

①有一个分区列表，即能被切分，可并行。

②由一个函数计算每一个分片

③容错机制，对其他RDD的依赖（宽依赖和窄依赖），但并非所有RDD都要依赖。

RDD每次transformations（转换）都会生成一个新的RDD，两者之间会形成依赖关系。在部分分区数据丢失时，可通过依赖关系重新计算丢失的数据。

④key-value型的RDD是根据哈希来分区的，控制Key分到哪个reduce。

⑤每一分片计算优先位置，比如HDFS的block的所在位置应该是优先计算的位置。

3、概述一下spark中的常用算子区别（map、mapPartitions、foreach、foreachPartition）

map	遍历RDD，将函数f应用于每一个元素，返回新的RDD	transformation算子
mapPartitions	用于遍历操作RDD中的每一个分区，返回生成一个新的RDD	transformation
collect	将RDD元素送回Master并返回List类型	Action
foreach	用于遍历RDD,将函数f应用于每一个元素，无返回值	action算子
foreachPartition	用于遍历操作RDD中的每一个分区。无返回值	action算子
总结	一般使用mapPartitions或者foreachPartition算子比map和foreach更加高效，推荐使用。

4、谈谈spark中的宽窄依赖

RDD和它依赖的父RDD的关系有两种不同的类型，即窄依赖和宽依赖。
宽依赖：指的是多个子RDD的Partition会依赖同一个父RDD的Partition分区【需要shuffle，与其他RDD交换资料】例如 groupByKey、 reduceByKey、 sortByKey等操作会产生宽依赖，会产生shuffle
窄依赖：指的是每一个父RDD的Partition最多被子RDD的一个Partition分区使用。【原地变换，不需要shuffle】例如map、filter、union等操作会产生窄依赖

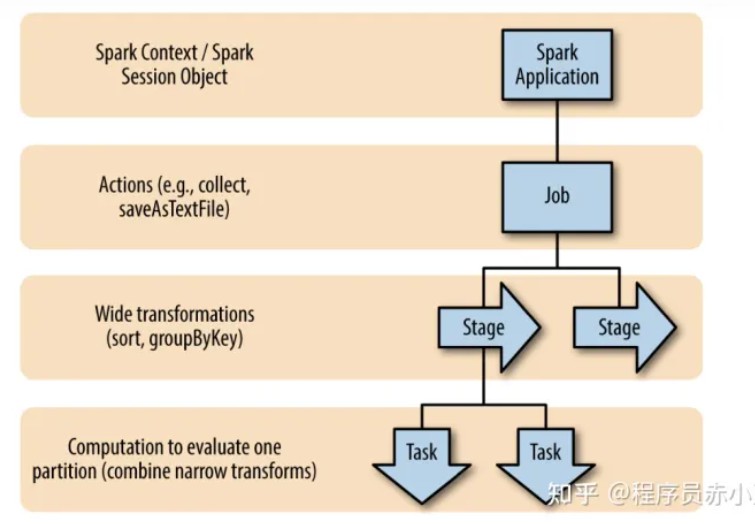
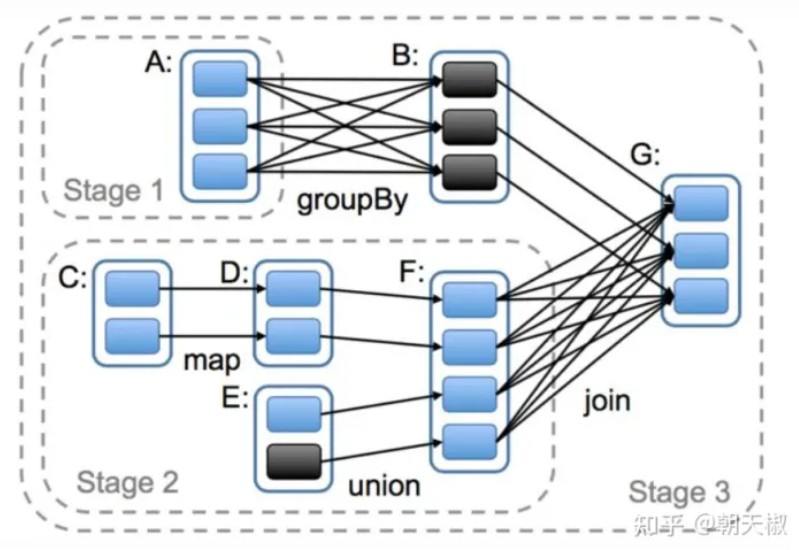
5、spark中如何划分stage

Stage划分的依据就是宽依赖，何时产生宽依赖，例如reduceByKey,groupByKey的算子，会导致宽依赖的产生。

先介绍什么是RDD中的宽窄依赖，
然后在根据DAG有向无环图进行划分，从当前job的最后一个算子往前推，遇到宽依赖，那么当前在这个批次中的所有算子操作都划分成一个stage,
然后继续按照这种方式在继续往前推，如在遇到宽依赖，又划分成一个stage,一直到最前面的一个算子。
最后整个job会被划分成多个stage,而stage之间又存在依赖关系，后面的stage依赖于前面的stage。

五、代码学习

1. 建立RDD

创建RDD的两种方法：

1 读取一个数据集(SparkContext.textFile()) : lines = sc.textFile(“README.md”)
2 读取一个集合(SparkContext.parallelize()) : lines = sc.paralelize(List(“pandas”,”i like pandas”))

#take操作将前若干个数据汇集到Driver，相比collect安全

# 创建RDD
# 从并行集合创建
pairRDD=sc.parallelize([('a',7),('a',2),('b',2)]) # key-value对RDD
rdd1=sc.parallelize([1,2,3,4,5])
rdd2=sc.parallelize(range(100))

#collect操作将数据汇集到Driver,数据过大时有超内存风险
all_data = rdd.collect()
all_data

#take操作将前若干个数据汇集到Driver，相比collect安全
rdd = sc.parallelize(range(10),5) 
part_data = rdd.take(4)
part_data

#takeSample可以随机取若干个到Driver,第一个参数设置是否放回抽样
rdd = sc.parallelize(range(10),5) 
sample_data = rdd.takeSample(False,10,0)
sample_data

#first取第一个数据
rdd = sc.parallelize(range(10),5) 
first_data = rdd.first()
print(first_data)

#count查看RDD元素数量
rdd = sc.parallelize(range(10),5)
data_count = rdd.count()
print(data_count)

从text中读取，read.text

从csv中读取:read.csv

从json中读取：read.json

2. RDD与Dataframe的转换

（1）dataframe转换成rdd：

法一：datardd = dataDataframe.rdd

法二：datardd = sc.parallelize(_)

（2）rdd转换成dataframe：

dataDataFrame = spark.createDataFrame(datardd)

3. rdd函数

mapReduce	说明
`rdd.map(func)`	将函数应用于RDD中的每个元素并返回
`rdd.mapValues(func)`	不改变key，只对value执行map
`rdd.flatMap(func)`	先map后扁平化返回
`rdd.flatMapValues(func)`	不改变key，只对value执行flatMap
`rdd.reduce(func)`	合并RDD的元素返回
`rdd.reduceByKey(func)`	合并每个key的value
`rdd.foreach(func)`	用迭代的方法将函数应用于每个元素
`rdd.keyBy(func)`	执行函数于每个元素创建key-value对RDD

pairRDD=sc.parallelize([('a',7),('a',2),('b',2)]) # key-value对RDD
rdd1=sc.parallelize([1,2,3,4,5])
rdd2=sc.parallelize(range(100))
>>> rdd1.map(lambda x:x+1).collect()
[2,3,4,5,6]
>>> rdd1.reduce(lambda x,y : x+y)
15
>>> rdd1.keyBy(lambda x:x%2).collect()
[(1,1),(0,2),(1,3),(0,4),(1,5)]
>>> pairRDD.mapValues(lambda x:x+1).collect()
[('a',8),('a',3),('b',3)]
>>> pairRDD.reduceByKey(lambda x,y : x+y).collect()
[('a',9),('b',2)]
>>> names=sc.parallelize(['Elon Musk','Bill Gates','Jim Green'])
>>> names.map(lambda x:x.split(' ')).collect()
[('Elon','Musk'),('Bill','Gates'),('Jim','Green')]
>>> names.flatMap(lambda x:x.split(' ')).collect()
['Elon','Musk','Bill','Gates','Jim','Green']

（1）map操作

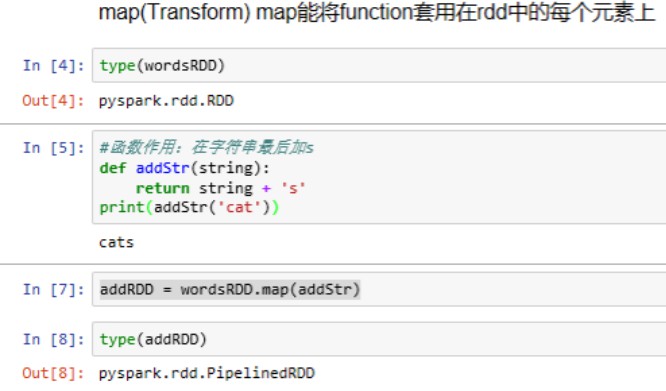
（2）collect操作

提取	说明
`rdd.collect()`	将RDD以列表形式返回
`rdd.collectAsMap()`	将RDD以字典形式返回
`rdd.take(n)`	提取前n个元素
`rdd.takeSample(replace,n,seed)`	随机提取n个元素
`rdd.first()`	提取第1名
`rdd.top(n)`	提取前n名
`rdd.keys()`	返回RDD的keys
`rdd.values()`	返回RDD的values
`rdd.isEmpty()`	检查RDD是否为空

pairRDD=sc.parallelize([('a',7),('a',2),('b',2)]) # key-value对RDD
>>> pairRDD.collectAsMap()
{'a': 2,'b': 2}
>>> pairRDD.keys().collect()
['a','a','b']
>>> pairRDD.values().collect()
[7,2,2]

分组和聚合	说明
`rdd.groupBy(func)`	将RDD元素通过函数变换分组为key-iterable集
`rdd.groupByKey()`	将key-value元素集分组为key-iterable集
`rdd.aggregate(zeroValue,seqOp,combOp)`	在驱动器上执行最终聚合，如果执行器的结果太大，则会导致驱动器出现内存错误并最终让程序崩溃。第一个函数执行分区内聚合。第二个函数执行分区间聚合。
depth = 3 rdd.treeAggregate(0, maxFunc, addFunc, depth)	基于不同的实现方法可以得到与aggregate相同的结果，创建从执行器到执行器传输结果的树，最后再执行最终聚合。多层级的形式确保驱动器在聚合过程中不会耗尽内存，这些基于树的实现通常会提高某些操作的稳定性。
`rdd.aggregateByKey(zeroValue,seqOp,combOp)`	此函数与aggregate基本相同，但是基于key聚合而非基于分区聚合。起始值和函数的属性配置也都相同
rdd.combineByKey	不仅可以指定聚合函数，还可以指定一个合并函数。该合并函数针对某个key进行操作，并根据某个函数对value合并，然后合并各个合并器的输出结果并得出最终结果。
`rdd.fold(zeroValue,func)`
`rdd.foldByKey(zeroValue,func)`	使用满足结合律函数和中性的“零值”合并每个key的value，支持多次累积到结果，并且不能更改结果（0为加法，1为乘法）

pairRDD=sc.parallelize([('a',7),('a',2),('b',2)]) # key-value对RDD
rdd1=sc.parallelize([1,2,3,4,5])
rdd2=sc.parallelize(range(100))
>>> rdd1.groupBy(lambda x: x % 2).mapValues(list).collect()
[(0,[2,4]),(1,[1,3,5])]
>>> pairRDD.groupByKey().mapValues(list).collect()
[('a',[7,2]),('b',[2])]

更好的解决方案：reduceByKey,非groupBykey
reduceByKey能够直接将资料根据key值聚合，减少多余的交换（shuffle）动作。reduce发生在每个分组，并且不需要将所有内容放在内存中

避免使用groupbykey，如果数据量过大，会造成内存溢出。每个执行器在执行函数之前必须在内存中保存一个key对应的所有value。

spark中groupByKey 、aggregateByKey、reduceByKey 有什么区别？使用上需要注意什么？

（1）groupByKey()是对RDD中的所有数据做shuffle,根据不同的Key映射到不同的partition中再进行aggregate。

（3） distinct()也是对RDD中的所有数据做shuffle进行aggregate后再去重。

（2）aggregateByKey()是先对每个partition中的数据根据不同的Key进行aggregate，然后将结果进行shuffle，完成各个partition之间的aggregate。因此，和groupByKey()相比，运算量小了很多。

（4）reduceByKey()也是先在单台机器中计算，再将结果进行shuffle，减小运算量

选择数据	说明
`rdd.sample(replace,frac,seed)`	抽样
`rdd.filter(func)`	筛选满足函数的元素(变换)
`rdd.distinct()`	去重


rdd1=sc.parallelize([1,2,3,4,5])
rdd2=sc.parallelize(range(100))
>>> rdd2.sample(False,0.8,seed=42)
>>> rdd1.filter(lambda x:x%2==0).collect()
[2,4]

排序	说明
`rdd.sortBy(func,ascending=True)`	按RDD元素变换后的值排序
`rdd.sortByKey(ascending=True)`	按key排序

统计	说明
`rdd.count()`	返回RDD中的元素数
`rdd.countByKey()`	按key计算RDD元素数量
`rdd.countByValue()`	按RDD元素计算数量
`rdd.sum()`	求和
`rdd.mean()`	平均值
`rdd.max()`	最大值
`rdd.min()`	最小值
`rdd.stdev()`	标准差
`rdd.variance()`	方差
`rdd.histograme()`	分箱（Bin）生成直方图
`rdd.stats()`	综合统计（计数、平均值、标准差、最大值和最小值）

pairRDD=sc.parallelize([('a',7),('a',2),('b',2)]) # key-value对RDD
>>> pairRDD.count()
3
>>> pairRDD.countByKey()
defaultdict(<type 'int'>,{'a':2,'b':1})
>>> pairRDD.countByValue()
defaultdict(<type 'int'>,{('b',2):1,('a',2):1,('a',7):1})
>>> rdd2.histogram(3)
([0,33,66,99],[33,33,34])

连接运算	说明
`rdd.union(other)`	并集(不去重)
`rdd.intersection(other)`	交集(去重)
`rdd.subtract(other)`	差集(不去重)
`rdd.cartesian(other)`	笛卡尔积
`rdd.subtractByKey(other)`	按key差集
`rdd.join(other)`	内连接
`rdd.leftOuterJoin(other)`	左连接
`rdd.rightOuterJoin(other)`	右连接
rdd.cogroup(rdd1)	连接
rdd.zip(rdd1)	组合两个zip, 将两个RDD的元素对应的匹配在一起，要求两个RDD的元素个数相同，且两个RDD的分区数也相同，结果会生成一个PairRDD

>>> rdd1=sc.parallelize([1,1,3,5])
>>> rdd2=sc.parallelize([1,3])
>>> rdd1.union(rdd1).collect()
[1,1,3,5,1,1,3,5]
>>> rdd1.intersection(rdd2).collect()
[1,3]
>>> rdd1.subtract(rdd2).collect()
[5]
>>> rdd2.cartesian(rdd2).collect()
[(1,1),(1,3),(3,1),(3,3)]
>>> rdd1=sc.parallelize([('a',7),('a',2),('b',2)])
>>> rdd2=sc.parallelize([('b','B'),('c','C')])
>>> rdd1.subtractByKey(rdd2).collect()
[('a',7),('a',2)]
>>> rdd1.join(rdd2).collect()
[('b',(2,'B'))]

>>> numPange = sc.parallelize(range(10), 2)
words.zip(numRange).collect()
'''
结果：
[('Spark', 0), 
('The', 1)
]
'''

持久化	说明
`rdd.persist()`	标记为持久化
`rdd.cache()`	等价于`rdd.persist(MEMORY_ONLY)`
`rdd.unpersist()`	释放缓存

cache后面能不能接其他算子,它是不是action操作？

Cache后可以接其他算子，但是接了算子之后，起不到缓存的作用，因为会重复出发cache。

Cache不是action操作。

cache和pesist有什么区别？

（1）cache和persist都是用于将一个RDD进行缓存的，这样在之后使用的过程中就不需要重新计算了，可以大大节省程序运行时间；

（2）cache只有一个默认的缓存级别MEMORY_ONLY ，cache调用了persist，而persist可以根据情况设置其它的缓存级别；

（3）executor执行的时候，默认60%做cache，40%做task操作，persist最根本的函数，最底层的函数

Spark为什么要持久化，一般什么场景下要进行persist操作？

为什么要进行持久化？

spark所有复杂一点的算法都会有persist身影,spark默认数据放在内存，spark很多内容都是放在内存的，非常适合高速迭代，1000个步骤

只有第一个输入数据，中间不产生临时数据，但分布式系统风险很高，所以容易出错，就要容错，rdd出错或者分片可以根据血统算出来，如果没有对父rdd进行persist 或者cache的化，就需要重头做。

以下场景会使用persist

1）某个步骤计算非常耗时，需要进行persist持久化

2）计算链条非常长，重新恢复要算很多步骤，很好使，persist

3）checkpoint所在的rdd要持久化persist，

lazy级别，框架发现有checnkpoint，checkpoint时单独触发一个job，需要重算一遍，checkpoint前

要持久化，写个rdd.cache或者rdd.persist，将结果保存起来，再写checkpoint操作，这样执行起来会非常快，不需要重新计算rdd链条了。checkpoint之前一定会进行persist。

4）shuffle之后为什么要persist，shuffle要进性网络传输，风险很大，数据丢失重来，恢复代价很大

5）shuffle之前进行persist，框架默认将数据持久化到磁盘，这个是框架自动做的。

分区	说明
`rdd.getNumPartitions()`	获取RDD分区数
`rdd.repartition(n)`	新建一个含n个分区的RDD，对数据进行重新分区，跨节点的分区会执行shuffle操作。对于map和filter操作，增加分区可以提高并行度。
`rdd.coalesce(n)`	将RDD中的分区减至n个, coalesce有效折叠(collapse)同一工作节点上的分区，以便在重新分区时避免数据洗牌(shuffle)。存储words变量的RDD当前有两个分区，可以使用coalsece将其折叠为一个分区。
`rdd.partitionBy(key,func)`	自定义分区
rdd.repartitionAndSortWithinPartitions	将对数据重新分区，并指定每个输出分区的顺序。

文件系统读写

# 读取
rdd=sc.textFile('hdfs://file_path')  # 从hdfs集群读取
rdd=sc.textFile('file_path') 
rdd=sc.textFile('file:///local_file_path') # 从本地文件读取
# 保存
rdd.saveAsTextFile('hdfs://file_path')
rdd.saveAsTextFile('file_path') # hdfs路径
rdd.saveAsTextFile('file:///local_file_path')

1.Spark简介

发表于 2023-03-09 | 分类于大数据， Spark

本文仅做学习总结，如有侵权立删

https://blog.csdn.net/weixin_42331985/article/details/124126019

https://zhuanlan.zhihu.com/p/396809439

https://blog.csdn.net/czz1141979570/article/details/105877261/

[TOC]

Spark生态架构图

Spark简介

1. 概念

Spark：基于内存的迭代式计算引擎。

RDD：Resillient Distributed Dataset（弹性分布式数据集），是分布式内存的一个抽象概念。

DAG：Directed Acyclic Graph（有向无环图），反映RDD之间的依赖关系。

Executor：是运行在工作节点（WorkerNode）的一个进程，负责运行Task

应用（Application）：用户编写的Spark应用程序

任务（ Task ）：运行在Executor上的工作单元(线程)

作业（ Job ）：一个作业包含多个RDD及作用于相应RDD上的各种操作

阶段（ Stage ）：是作业的基本调度单位，一个作业会分为多组任务，每组任务被称为阶段，或者也被称为任务集合，代表了一组关联的、相互之间没有Shuffle依赖关系的任务组成的任务集, 下图为DAG划分Stage过程：

2. 组件关系

当执行一个Application时，Driver会向Yarn申请资源，启动Executor（Worker），并向Executor发送代码和文件，执行任务，任务结束后执行结果会返回给任务控制节点，或者写到HDFS/Hive等。

1 Application = 1 Driver + 多 Job

1 Job（多个 RDD + RDD的操作） = 多个Stage

1 Stage = 多个Task

3. 运行流程

（1）概念层级

解释1：

一个Spark提交时，由Driver运行main方法创建一个SparkContext，由SparkContext负责和Yarn的通信、资源的申请、任务的分配和监控等。

SparkContext会向Yarn注册并申请运行Executor的资源。

Yarn为Executor分配资源，启动Executor进程，Executor发送心跳到Yarn上

SparkContext根据RDD的依赖关系构建DAG图，DAG调度解析后将图分解成多个Stage，并计算出之间的依赖关系，将这些Job集提交给Task调度器处理。Executor向SparkContext申请Task，Task调度器将Task分发给Executor运行，同时，SparkContext将Application代码发放给Executor。

任务在Executor上运行，结果反馈给Job调度器，再反馈给DAG调度器，运行完毕后写入数据并释放所有资源。

在这里插入图片描述

解释2：

每个 worker 节点包含一个或者多个 executor，一个 executor 中又包含多个 task。task 是真正实现并行计算的最小工作单元。

Driver
Driver 是一个 Java 进程，负责执行 Spark 任务的 main 方法，它的职责有：

执行用户提交的代码，创建 SparkContext 或者 SparkSession

将用户代码转化为Spark任务（Jobs）

创建血缘（Lineage），逻辑计划（Logical Plan）和物理计划（Physical Plan)

在 Cluster Manager 的辅助下，把 task 任务分发调度出去

跟踪任务的执行情况

Spark Context/Session
它是由Spark driver创建，每个 Spark 应用对应一个。程序和集群交互的入口。可以连接到 Cluster Manager

Cluster Manager
负责部署整个Spark 集群，包括上面提到的 driver 和 executors。具有以下几种部署模式

Standalone 模式

YARN

Mesos

Kubernetes

Executor
一个创建在 worker 节点的进程。一个 Executor 有多个 slots(线程) 可以并发执行多个 tasks。

负责执行spark任务，把结果返回给 Driver

可以将数据缓存到 worker 节点的内存

一个 slot 就是一个线程，对应了一个 task

（2）代码层级

Spark 有懒加载的特性，也就是说 Spark 计算按兵不动，直到遇到 action 类型的 operator 的时候才会触发一次计算。

DAG

Spark Job如何执行，都是由这个 DAG 来管的，包括决定 task 运行在什么节点

Spark Job

每个Spark Job 对应一个action

Stages

每个 Spark Job 包含一系列 stages

Stages 按照数据是否需要 shuffle 来划分（宽依赖）

Stages 之间的执行是串行的（除非stage 间计算的RDD不同）

因为 Stages 是串行的，所以 shuffle 越少越好

Tasks

每个 stage 包含一系列的 tasks

Tasks 是并行计算的最小单元

一个 stage 中的所有 tasks 执行同一段代码逻辑，只是基于不同的数据块

一个 task 只能在一个executor中执行，不能是多个

一个 stage 输出的 partition 数量等于这个 stage 执行 tasks 的数量

Partition

Spark 中 partition（分区）可以理解为内存中的一个数据集

一个 partition 对应一个 task，一个 task 对应一个 executor 中的一个 slot，一个 slot 对应物理资源是一个线程 thread

1 partition = 1 task = 1 slot = 1 thread

(3) spark中Master与Worker区别及Driver与Executor区别

Master和Worker是Spark的守护进程，即Spark在特定模式下正常运行所必须的进程。Driver和Executor是临时程序，当有具体任务提交到Spark集群才会开启的程序。

了解 Spark中的master、worker和Driver、Executor

每个Worker上存在一个或者多个ExecutorBackend 进程。每个进程包含一个Executor对象，该对象持有一个线程池，每个线程可以执行一个task。
每个application包含一个 driver 和多个 executors，每个 executor里面运行的tasks都属于同一个application。
每个Worker上存在一个或者多个ExecutorBackend 进程。
每个进程包含一个Executor对象，该对象持有一个线程池，每个线程可以执行一个task

4. DAGScheduler具体流程

DAG负责的是将RDD中的数据依赖划分为不同可以并行的宽依赖task，这些不同的task集合统称为stage，最后将这些stage推送给TaskScheduler进行调度，DAG的具体划分过程如下所示：

窄依赖经历的是map、filter等操作没有进行相关的shuffle，而宽依赖则通常都是join等操作需要进行一定的shuffle意味着需要打散均匀等操作

1 stage是触发action的时候 从后往前划分 的，所以本图要从RDD_G开始划分。

2 RDD_G依赖于RDD_B和RDD_F，随机决定先判断哪一个依赖，但是对于结果无影响。

3 RDD_B与RDD_G属于窄依赖，所以他们属于同一个stage，RDD_B与老爹RDD_A之间是宽依赖的关系，所以他们不能划分在一起，所以RDD_A自己是一个stage1

4 RDD_F与RDD_G是属于宽依赖，他们不能划分在一起，所以最后一个stage的范围也就限定了，RDD_B和RDD_G组成了Stage3

5 RDD_F与两个爹RDD_D、RDD_E之间是窄依赖关系，RDD_D与爹RDD_C之间也是窄依赖关系，所以他们都属于同一个stage2

6 执行过程中stage1和stage2相互之间没有前后关系所以可以并行执行，相应的每个stage内部各个partition对应的task也并行执行

7 stage3依赖stage1和stage2执行结果的partition，只有等前两个stage执行结束后才可以启动stage3.

8 我们前面有介绍过Spark的Task有两种：ShuffleMapTask和ResultTask，其中后者在DAG最后一个阶段推送给Executor，其余所有阶段推送的都是ShuffleMapTask。在这个案例中stage1和stage2中产生的都是ShuffleMapTask，在stage3中产生的ResultTask。

9 虽然stage的划分是从后往前计算划分的，但是依赖逻辑判断等结束后真正创建stage是从前往后的。也就是说如果从stage的ID作为标识的话，先需要执行的stage的ID要小于后需要执行的ID。就本案例来说，stage1和stage2的ID要小于stage3，至于stage1和stage2的ID谁大谁小是随机的，是由前面第2步决定的。

5. MR和spark区别

（1）中间结果输出：

MapReduce：读–处理–写磁盘–读–处理–写磁盘（中间结果落地，即存入磁盘）

spark：读–处理–处理–（需要的时候）写磁盘（中间结果存入内存）

减少落地时间，速度快

（2）数据格式：

MapReduce：从DB中读取数据再处理

spark：采用弹性分布式数据结构RDD存储数据

（3）容错性：

Spark：采用RDD存储数据，若数据集丢失，可重建。

（4）通用性：

MapReduce：只提供map和reduce两种操作。

spark：提供很多数据集操作类型（transformations、actions）【transformations包括map\filter\

Groupbykey\sort等，action包括reduce、save、collect、lookup等】

（5）执行策略

MapReduce：数据shuffle前需排序

spark：不是所有场景都要排序

6、spark1.x和spark2.x的区别

Spark1.x：采用SparkContext作为进入点

Spark2.x：SparkSession 是 Spark SQL 的入口。

采用SparkSession作为进入点，SparkSession可直接读取各种资料源，可直接与Hive元数据沟通，同时包含设定以及资源管理功能。

7. spark 应用执行模式

（1）local模式

local 模式主要是用于本地代码测试操作

本质上就是一个单进程程序, 在一个进程中运行多个线程

类似于pandas , 都是一个单进程程序, 无法处理大规模数据, 只需要处理小规模数据

（2）standalone：

Spark Standalone模式：该模式是不借助于第三方资源管理框架的完全分布式模式。Spark 使用自己的 Master 进程对应用程序运行过程中所需的资源进行调度和管理；对于中小规模的 Spark 集群首选 Standalone 模式。目前Spark 在 Standalone 模式下主要是借助 Zookeeper 实现单点故障问题；思想也是类似于 Hbase Master 单点故障解决方案。

（3）YARN

该模式是借助于第三方资源管理框架 Yarn 的完全分布式模式。Spark 作为一个提交程序的客户端将 Job 任务提交到 Yarn 上；然后通过 Yarn 来调度和管理 Job 任务执行过程中所需的资源。需要此模式需要先搭建 Yarn 集群，然后将 Spark 作为 Hadoop 中的一个组件纳入到 Yarn 的调度管理下，这样将更有利于系统资源的共享。

8. 提交任务方法

（1）spark shell

spark-shell 是 Spark 自带的交互式 Shell 程序，方便用户进行交互式编程，用户可以在该命令行下用 Scala 编写 spark 程序。

应用场景

通常是以测试为主

所以一般直接以./spark-shell启动，进入本地模式测试

local方式启动：./spark-shell

standalone集群模式启动：./spark-shell –master spark://master:7077

yarn client模式启动：./spark-shell –master yarn-client

（2）spark submit

使用spark 自带的spark-submit工具提交任务

程序一旦打包好，就可以使用 bin/spark-submit 脚本启动应用了。这个脚本负责设置 spark 使用的 classpath 和依赖，支持不同类型的集群管理器和发布模式。

它主要是用于提交编译并打包好的Jar包到集群环境中来运行，和hadoop中的hadoop jar命令很类似，hadoop jar是提交一个MR-task,而spark-submit是提交一个spark任务，这个脚本可以设置Spark类路径（classpath）和应用程序依赖包，并且可以设置不同的Spark所支持的集群管理和部署模式。相对于spark-shell来讲它不具有REPL(交互式的编程环境)的，在运行前需要指定应用的启动类，jar包路径,参数等内容。

9. 参数配置：

参数名参数说明

-class 应用程序的主类，仅针对 java 或 scala 应用
-master master 的地址，提交任务到哪里执行，例如 local,spark://host:port, yarn, local
-deploy-mode 在本地 (client) 启动 driver 或在 cluster 上启动，默认是 client
-name 应用程序的名称，会显示在Spark的网页用户界面
-jars 用逗号分隔的本地 jar 包，设置后，这些 jar 将包含在 driver 和 executor 的 classpath 下
-packages 包含在driver 和executor 的 classpath 中的 jar 的 maven 坐标
-exclude-packages 为了避免冲突而指定不包含的 package
-repositories 远程 repository
-conf PROP=VALUE 指定 spark 配置属性的值，例如 -conf spark.executor.extraJavaOptions=”-XX:MaxPermSize=256m”
-properties-file 加载的配置文件，默认为 conf/spark-defaults.conf
-driver-memory Driver内存，默认 1G
-driver-java-options 传给 driver 的额外的 Java 选项
-driver-library-path 传给 driver 的额外的库路径
-driver-class-path 传给 driver 的额外的类路径
-driver-cores Driver 的核数，默认是1。在 yarn 或者 standalone 下使用
-executor-memory 每个 executor 的内存，默认是1G
-total-executor-cores 所有 executor 总共的核数。仅仅在 mesos 或者 standalone 下使用
-num-executors 启动的 executor 数量。默认为2。在 yarn 下使用
-executor-core 每个 executor 的核数。在yarn或者standalone下使用

过拟合

发表于 2023-02-26 | 分类于机器学习，基础

本篇博客仅作为学习,如有侵权必删。

过拟合

一、概念

过拟合：模型对于训练数拟合呈过当的情况，反映到评估指标上，就是模型在训练集上表现很好，测试集和新数据上表现较差。

欠拟合：模型在训练和和预测时表现都不好的情况。

正则化

发表于 2023-02-26 | 分类于机器学习，基础

本篇博客仅作为学习,如有侵权必删。

正则化/惩罚项

一、概念

（1）范数：

（2）方差和偏差：

Error = Bias + Variance

Error反映的是整个模型的准确度，

Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，

Variance反映的是模型每一次输出结果与模型输出期望之间的误差（描述的是样本上训练的模型在测试集上的表现。），即模型的稳定性。

欠拟合是高bias，过拟合是高variance。

（3）正则化的目的：减少模型参数大小或者参数数量，缓解过拟合。

正则化的作用是给模型加一个先验，lasso(l1)认为模型是拉普拉斯分布，ridge(l2)认为是高斯分布，正则项对应参数的协方差，协方差越小，这个模型的variance越小，泛化能力越强，也就抵抗了过拟合。

（4）正则化通用形式：

Loss_with_regularization = loss(w,x) + λf(w)

正则化恒为非负

f(w)不能为负数，若其为负数，Loss(w,x)+λf(x)本来尽可能想让其变小，那f(x)为负数，f(x)绝对值会越学越大。

(5) 正则化方法：L1正则、L2正则、Dropout正则

二、从数学角度解释正则化为什么能提升模型的泛化能力；【奥卡姆剃刀：简单就好】

过拟合就是模型在学习训练样本时将噪声异常值也学习得非常好，使得模型参数过多，模型较复杂，给参数加上一个先验约束，可降低过拟合。

三、L1和L2范数各有什么特点以及相应的原因？L1和L2的区别与应用场景；

区别：L1假设参数服从拉普拉斯分布，L2则符合高斯分布；

L1范数更容易产生稀疏的权重，L2范数更容易产生分散的权重。

原因：（L1稀疏的原因，L2不稀疏的原因）【几何、公式两个角度】

场景：具有高维的数据特征时采用L1正则效果好一点。因为L1具有稀疏性。

四、解释L1范数更容易产生稀疏的权重，L2不的原因：

（1）几何角度

L2正则项约束后的解空间是圆形，L1正则项约束后的解空间是多方形，L1易在角点发生交点，从而产生稀疏解。

绿色等高线代表未施加正则化的代价函数，菱形和圆形分别代表L1和L2正则化约束，L1-ball 与L2-ball的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的”等高线”除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性。相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小

（2）公式角度：（拉格朗日求导）

深度学习花书7.1节（202页左右）。带L1正则化的最优参数w=sign(w) max{|w|- a/H , 0}，其中w代表未正则化的目标函数的最优参数，H代表海森矩阵，a是正则化系数，只要a足够大，w就会在更大区间范围内使w变为0，而带L2正则化的最优参数w=H/(H+a)▪w,只要w不为0，w也不为0.

1、稀疏性的约束：

L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

2、不好求解，松弛为L1，L2：

3、拉格朗日

（3）贝叶斯先验

L1正则化相当于对模型参数w引入了拉普拉斯先验，L2正则化相当于引入了高斯先验，而拉普拉斯先验使参数为0的可能性更大。

L1正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出。

L2正则化可通过假设权重w的先验分布为高斯分布，由最大后验概率估计导出。

详细解释： https://blog.csdn.net/m0_38045485/article/details/82147817

概率论

发表于 2023-02-26 | 分类于机器学习，先导知识，概率论基本知识

本篇博客仅作为学习,如有侵权必删。

一、均值、方差、协方差

期望/均值：实验中每次可能结果的概率乘其结果的总和。
- E(X)=∑xP(X), x表示随机变量的取值，P(X)表示随机变量X=x的概率。
方差：概率分布的数据期望，反映了随机变量取值的变异程度。
- D(x ) = E{[X-E(X)]^2} =E(X^2) - [ E(X)]^2

协方差：度量两个随机变量关系的统计量

标准化

发表于 2023-02-26 | 分类于机器学习，基础

本篇博客仅作为学习,如有侵权必删。

一、BN批标准化

1、BN的基本动机

（初始数据分布一致）神经网络训练过程的本质是学习数据分布，如果训练数据与测试数据的分布不同将大大降低网络的泛化能力，因此我们需要在训练开始前对所有输入数据进行归一化处理。
（中间数据分布一致）然而随着网络训练的进行，每个隐层的参数变化使得后一层的输入发生变化，从而每一批训练数据的分布也随之改变，致使网络在每次迭代中都需要拟合不同的数据分布，增大训练的复杂度以及过拟合的风险。

原因在于神经网络学习过程本质上是为了学习数据的分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另一方面，一旦在mini-batch梯度下降训练的时候，每批训练数据的分布不相同，那么网络就要在每次迭代的时候去学习以适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对所有训练数据做一个Normalization预处理的原因。

2、 BN的原理

BN首先是把所有的样本的统计分布标准化，降低了batch内不同样本的差异性，然后又允许batch内的各个样本有各自的统计分布。

BN是针对每一批数据，在网络的每一层输入之前增加归一化处理（均值为0，标准差为1），将所有批数据强制在统一的数据分布下，即对该层的任意一个神经元（假设为第k维）x^(k) 采用如下公式:

广告校准

发表于 2023-02-25 | 分类于计算广告，校准广告

本篇博客仅作为学习,如有侵权必删。

https://zhuanlan.zhihu.com/p/460061332

https://zhuanlan.zhihu.com/p/582530785

https://zhuanlan.zhihu.com/p/398235467

广告校准

1. 业务背景

广告三大角色：广告主、媒体、DSP

ctr : (Click Through Rate) 点击率 = click / show，曝光广告中用户点击的概率。

cvr: (Conversion Rate) 转化率 = order / click，点击广告中用户转化的概率。（如注册，激活，创角等）

cpa：(Cost per Action) 转化成本 = cost / order, 表示广告主每获得一个转化需付的成本。

ecpm / rpm：= ctr cvr cpa

ecpm : 对广告主来说，(Effective Cost Per Mile) 每千次展示的有效费用。

rpm：对DSP来说，(Revenue Per Mile)每千次展示的收入。

pctr: (Predict CTR) 预估点击率

pcvr: (Predict CVR) 预估转化率

2. 面临的问题

（1）模型准确性存在偏差，受限于

实际分布和离线分布的差异

模型学习能力

（2）预估模型的准确性度量

AUC：仅作为排序指标，无法度量预估值的大小准确性

COPC：（Click On Predict Click) = sum( 实际ctr) / sum(pctr)

用于评估某段细分的流量模型预估值是否偏差较大。

（3）校准评价指标：

PCOC：（predict click over click）COPC是相反的指标。

cal-N：（calibration-N）

cal-N将样本集合分桶后分别计算PCOC，并计算与1的偏差作为标准误差。举个例子，将pctr根据值大小划分为多个桶，每个桶为一个簇，计算每个簇的PCOC及其与1的偏差数学公式:

GC-N：（grouped calibration-N）

在具体业务场景下，有时会重点关注某一维度下的校准效果(如广告计费维度)，GC-N可以解决这个问题，它可以在cal-N基础上自定义各维度权重。例如，下面这个式子定义了m个广告计划的GC-N 数学公式:

3. 校准算法

（1） Bias Correction：负采样率修正

原因：正负样本不均衡情况下，负采样通常可以提升模型的AUC精度，但pctr值会发生变化，与真实差距扩大。

校准公式：

因此可以计算出校准后的bias: b′=b+log(n)

代码：

注意在导出模型时，最终结果过完sigmoid，再进行bias_correct。

import math
def bias_correct(b, nr):
	"""
	nr: neg_sample_rate
	
	"""
    if nr < 1:
        return b + math.log(nr)
    else:
        return b

nr = 0.1 # 负采样率
last_op['bias'] = bias_correct(last_op['bias']， nr) # 纠正sigmoid后的bias

（2）校准算法—保序回归

解决模型高低估、模型over-confidence等问题。

def get_sir_calibration_model(pctr_list = [0.01,0.02,0.03,0.04], ctr_list = [0,1,0,1], bin_size = 0.01):
	sort_ctr_list = sorted(list(zip(pctr_list, ctr_list)), key = lambda x:x[0])
    bin_index = 0
    ind = 0
    n = len(ctr_list)
    cctr_res = []
    while ind < n:
        while (bin_index + bin_size) < sort_ctr_list[ind][0]:
            cctr_res.append(sort_ctr_list[ind][1])
            bin_index += 1
        if (bin_index + bin_size) == sort_ctr_list[ind][0]:
            cctr_res.append(sort_ctr_list[ind][1])
            ind += 1
            bin_index += bin_size
            continue
        if ind + 1== n:
            break
        tmp_cctr = sort_ctr_list[ind + 1][1]
        tmp_num = 1
        while ind + 1 < n and bin_index + bin_size > sort_ctr_list[ind][0]:
            tmp_cctr += sort_ctr_list[ind][1]
            tmp_num += 1
            ind += 1
        cctr_res.append(tmp_cctr/tmp_num)
        bin_index += bin_size

（3）校准算法3 —-SIR（保序回归平滑校准算法）

解决桶间数据稀疏问题

SIR算法是18年提出的，如上图所示，结合了Binning、Isotonic Regression和线性Scaling方法。

具体思想为：

进行保序回归。
使用单调平滑函数拟合模型预估值和实际点击率的映射关系（线性Scaling）就得到了校准函数。

该算法的优势在于充分利用了保序和平滑思想缓解了数据稀疏的问题。

（详细可见论文：Calibrating user response predictions in online advertising）。

（4）校准算法4—贝叶斯平滑SIR校准算法（Bayes-SIR)

Bayes-SIR解决冷启动问题。

beta分布：可以看作一个概率的概率分布

带你理解beta分布

贝叶斯平滑方法:（最早在雅虎的一篇论文里面中提出，用于解决数据稀疏问题下的点击率预估优化）。

在SIR算法应用中，发现广告计划投放初期校准效果明显差于平均水平，并在实际业务中造成以下问题：

1）影响新建计划初始阶段的投放表现；

2）影响强时效性广告的全生命周期效果；

3）小客户在整个投放周期里数据一直稀疏，得不到准确的校准，影响竞价公平性。

这是SIR校准算法的冷启动问题，采用了Bayes平滑的思想进行优化.

Bayes-SIR的算法思想：如上图所示，

从丰富的先验数据中估计出每个广告计划的点击率先验分布，
依据该先验知识求解出belta分布的参数α和β。
依据α和β和新观测到的少量数据，计算得到更准确的后验点击率。

这种估计方法能充分利用先验知识，具备置信程度过渡平滑的特点。

将贝叶斯平滑CTR估计过程替换掉SIR算法的朴素CTR统计逻辑即构成了具有冷启动问题优化效果的校准方法。

实际上线后，新广告的投放效果得到明显的提升。

梯度下降

发表于 2023-02-21 | 分类于机器学习，基础

本篇博客仅作为学习,如有侵权必删。

[TOC]

梯度下降

1. 重点

(1) 常用的优化方法：牛顿法、GD、拟牛顿法、共轭梯度法，之间的区别

(2) GD三种变形：BGD、SGD、MBGD

(3) 多种改进方法：Momentum、NAG、Adagrad、Adadelta、RMSProp、Adam

2. 概念

（1）常用的优化方法：直接法、迭代法（梯度下降、牛顿法、拟牛顿法、共轭梯度法）

（2）直接法（求解析解）：

求梯度，令梯度为0

（3）牛顿法：

（4） GD 梯度下降:

让变量沿着目标函数负梯度的方向移动，直到移动到极小值点。

从拉格朗日中值定理 / 泰勒展开一阶公式都可以推出损失函数下降最大的方向是梯度方向。

3. 梯度下降法和牛顿法的区别

牛顿法和梯度下降法对比：

从公式上看，牛顿法是二阶收敛，梯度下降是一阶收敛（局部最优），所以牛顿法就更快。

【如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。】

从几何上看，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

4. 三种变形

GD的三种变形：BGD、SGD、MBGD

这三种形式的区别就是取决于我们用多少数据来计算目标函数的梯度。

（1）Batch gradient descend【批量梯度下降】

定义：【采用整个训练数据集的数据计算损失函数对参数的梯度】
优点：全局最优解；易于并行实现；
缺点：大样本数据计算速度非常慢，不能投入新数据实时更新模型。
收敛：对于凸函数可以收敛到全局最优，对于非凸函数可以收敛到局部最优。

（2） Stochastic gradient descent【随机梯度下降】【适合在线更新】

定义：SGD 每次更新时对一个样本进行梯度更新。
优点：对于很大的数据集来说，可能会有相似的样本，这样 BGD在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本。
缺点：但是 SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。准确度下降，不易于并行实现。
收敛性：不一定每次更新朝着最优值方向，因为存在噪音点，局部最优。

（3）mini-batch GD【小批量梯度下降】：降低随机梯度的方差

【在更新每一参数时都使用一部分样本来进行更新】

‘

缺点：需要指定batch大小，收敛性不好。
一般batch取2的幂次能充分利用矩阵运算操作（32,64,128……）

三种方法的使用情况：

如果样本量比较小，采用批量梯度下降算法。如果样本太大，或者在线算法，使用随机梯度下降算法。在实际的一般情况下，采用小批量梯度下降算法。

GD具有的几个问题：

1、学习率选择【太小，收敛速度慢，太大，在最优值附近震荡】

2、学习率不固定【稀疏数据，学习率可增大】

3、（尤其SGD）对于非凸函数，易陷于局部最优值/鞍点。

5、优化方法

（1）动量Momentum【一般为SGD+momentum】

原理：因为SGD易陷于局部最优点或鞍点，一种帮助SGD在相关方向进行加速并抑制振荡的方法

momentum表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练开始时，由于梯度可能会很大，所以初始值一般选为0.5；当梯度不那么大时，一般改为0.9。
α是学习率，即当前batch的梯度多大程度上影响最终更新方向，跟普通的SGD含义相同。

优点：因此获得了更快的收敛性和减少了震荡。
缺点：这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。

向量乘积

发表于 2023-02-21 | 分类于机器学习，先导知识，向量乘积

本篇博客仅作为学习,如有侵权必删。

向量乘积

1. 内积

含义：两个向量的相似度/向量的夹角，标量。

向量a和向量b的余弦的相似度: 对内积进行了归一化

cosθ = 内积 / (|a| * |b| )

2. 哈达玛积

元素两两相乘。

[a1, b1, c1] * [a2, b2, c2] = [a1a2, b1b2, c1c2]

元素集的交互： [w1 a1a2, w2 b1b2, w3 *c1c2]

向量级别的交互：w [a1a2, b1b2, c1c2]

逻辑回归

发表于 2023-02-20 | 分类于机器学习，基础

本篇博客仅作为学习,如有侵权必删。

[TOC]

逻辑回归

1. LR重点

LR的重点：

目的：LR解决二分类问题。
输出结果：(0,1)之间的数值。
模型：线性模型 + sigmoid函数
- y_pred = sigmoid(W0+W1 x1 + … + Wn xn) = sigmoid(∑W^TX)
LR为何用sigmoid函数？ sigmoid的性质
损失函数：loss = -(∑y) log y_pred_i + (1-yi) log(1 - y_pred_i))
损失函数的推导：
求解方法：梯度下降

2. 概念

二分类：假设有一批训练样本集合X={x1,x2,…,xn},其中xi有a个属性，对这些样本分类属于0还是1？

伯努利分布：离散型概率分布，成功则随机变量取值为1，失败则为0，设置成功的概率为p,则失败的概率为1-p，N次实验后，成功期望是Np，方差为 Np(1-p)

期望/均值：实验中每次可能结果的概率乘其结果的总和。E(X)=∑xP(X), x表示随机变量的取值，P(X)表示随机变量X=x的概率。

方差：概率分布的数据期望，反映了随机变量取值的变异程度。D(x ) = E{[X-E(X)]^2}=E(X^2) - [ E(X)]^2

似然函数（联合概率密度函数）：

先验概率：根据以往经验和分析得到的概率。主观上的经验估计p(x)

似然函数：在给定参数θ情况下得到结果 X 的概率分布p(x|θ) 。

（给定输出x时，使得函数得到X概率最大的关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率，即L(θ|x) = P(X=x|θ)）

后验概率：在给定结果信息X的情况下得到参数 θ 的概率： p(θ|x) 。

梯度下降：一种求解模型的方法，后面细看。

LR：假设数据服从伯努利分布，通过极大化似然函数的方法，运用梯度下降来求解参数，达到将数据二分类的目的。

3. LR模型和损失函数

模型和损失函数得到的过程：

第①步：引入参数θ=（θ1，θ2……），对于样本加权θ^TX

第②步：引入logit函数：g(z)=1/(1+e^-z)，令z=θ^TX，故LR的模型：

假设样本服从的是伯努利分布（0-1分布）:

以上h的含义是：表示样本x属于类别1的概率，即P（y=1|x;θ）。则样本x属于类别0的概率为1-hθ(x)。

联合两个概率即为似然函数。

第③步：似然函数（联合概率密度函数）：

所有样本的似然函数：（令概率最大化）

第④步：损失函数（对数似然函数取反min）：交叉熵损失函数

4. 损失函数的来源推导

法一：假设服从伯努利分布，伯努利分布的极大似然估计

假设样本服从伯努利(0-1)分布,有：

法二：熵角度确定损失函数

KL散度（相对熵）：KL散度可以用来衡量两个分布之间的差异程度。若两者差异越小，KL散度越小，反之亦反。当两分布一致时，其KL散度为0。

相关概念请看：熵的章节

如果是两个随机变量P,Q，且其概率分布分别为p(x),q(x),则p相对q的相对熵为：

模型预估值分布和实际值分布的KL散度：（KL散度越小，表明两个分布越相似，即预估值越接近实际值）。

p log(p/q) = p logp - p* logq

其中， p logp是一个定值（实际值分布p = y_i，是固定的，0或1），- p logq是交叉熵，只要交叉熵较大，则KL散度就越小，预测值和实际值越相似。

交叉熵：令-p log q = -y_i log y_pred_i . (可扩展为多个： -（y1 log y_pred_1 + y2 log y_pred_2 + y3 * log y_pred_3.。。。)

法三、贝叶斯学派确定损失函数

贝叶斯公式：

贝叶斯学派有先验函数，频率学派仅考虑似然函数。

贝叶斯用上一次的后验当成下一次的先验与似然函数相乘，计算下一次的后验，不断迭代。

5. LR为何用sigmoid函数？

（1）数学上

1. 因为LR服从伯努利分布，伯努利分布转化为广义线性模型指数分布族形式里可推导出sigmoid函数

（2）概率上：

sigmoid自身性质，值域在（0,1）之间，满足概率的要求

（3）单调性：

若sigmoid不具备单调性，LR不可用其作为映射函数。

下图的g1 < g2的x指的是线性中的g=wx的值。若LR的映射函数不具备单调性，则同一个y值会对应两个g值。

因为x是给定的特征，则w没办法学习，因为LR是个记忆函数，在g1之前当学习w发现增大w1能让y接近高点（即在g1和g2之间）时，突然发现当w1更大时（大于g2），y越来越小，没办法沿着某些方向学习w值。

sigmoid具备单调性，则在使用redis存储参数w的key和value时，若推荐最终结果只涉及排序，则无需进行sigmoid计算，且若是离散特征，只需将x特征值为1对应的参数w相加得到最终值进行排序即可。又可以提高效率了。

sigmoid性质：

定义域：（-∞，+∞）

将任意input压缩到(0,1)之间，即值域为（0,1），符合概率定义

设f(x) = sigmoid(x), f(x)导数为f(x)*(1-f(x)), 对梯度下降有好处，前向传递时计算结果可以保留，BP时可以直接用来计算，加快速度

1/2处导数最大，两边梯度趋于饱和，容易发生梯度消失（作为激活函数的弊端）

不以原点为中心，BP时梯度下降更新慢，更新时以zigzag（折线）方式更新。（作为激活函数的弊端）

单调性，LR的映射函数如果没有单调性不行。

6.【为什么参数的梯度方向一致容易造成zigzag现象】

当所有梯度同为正或者负时，参数在梯度更新时容易出现zigzag现象。

zigzag现象如图4所示，不妨假设一共两个参数， w0 和 w1 ，紫色点为参数的最优解，蓝色箭头表示梯度最优方向，红色箭头表示实际梯度更新方向。

由于参数的梯度方向一致，要么同正，要么同负，因此更新方向只能为第三象限角度或第一象限角度，而梯度的最优方向为第四象限角度，也就是参数 w0 要向着变小的方向， w1 要向着变大的方向，在这种情况下，每更新一次梯度，不管是同时变小(第三象限角度)还是同时变大(第四象限角度)，总是一个参数更接近最优状态，另一个参数远离最优状态，因此为了使参数尽快收敛到最优状态，出现交替向最优状态更新的现象，也就是zigzag现象。

7. 梯度下降求解损失函数

梯度下降概念：根据loss求导，往

注意：这里梯度更新时用加号是因为max loss。非min loss的值。

8. LR的优缺点

优点：

1、形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。
2、模型效果不错。在工程上是可以接受的（作为baseline)，如果特征工程做的好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发的速度。
3、训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟，训练的速度可以通过堆机器进一步提高，这样我们可以在短时间内迭代好几个版本的模型。
4、资源占用小,尤其是内存。因为只需要存储各个维度的特征值。
5、方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)。
6、对稀疏数据比较友好。一个特征通过 one-hot : [0,0,1,……,0] ，LR是个记忆模型，将该特征扔进LR之后，会将x3=1（w3）记得很好，别的都为0了，但这样也容易过拟合。（gbm，深度模型这些都不太喜欢稀疏数据）

缺点:

准确率并不是很高。因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布。
很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好。
处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下，只能处理线性可分的数据，或者进一步说，处理二分类的问题。
逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归。
对模型中自变量多重共线性较为敏感，例如两个高度相关自变量同时放入模型，可能导致较弱的一个自变量回归符号不符合预期，符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量，以减少候选变量之间的相关性；
必须对缺失值处理

9. 扩展问题

线性回归与LR的本质区别：

【线形回归与逻辑回归的本质区别是前者用于回归后者用于分类，二者都是线形模型。】

什么情况下用LR【大规模样本下的线性二分类】

LR的损失函数的公式和函数

逻辑回归的损失函数为什么要使用极大似然函数作为损失函数？

【如果激活函数为sigmoid函数，使用均方误差作为损失函数的话为非凸函数，而使用对数损失函数为凸函数】

【损失函数一般有四种，平方损失函数、对数损失函数、铰链损失函数和绝对值损失函数。极大似然取对数之后相当于对数损失，在LR模型下，对数损失函数的训练求解参数速度是比较快的，不选平方损失函数是因为梯度更新的速度和sigmoid函数本身的梯度是相关的，这样训练会比较慢】

LR的推导过程

LR如何解决共线性，为什么深度学习不强调

【法1：岭回归（L2正则化）、

法2：主成分分析，

法3：共线性诊断常用的统计量：将所有回归中要用到的变量依次作为因变量、其他变量作为自变量进行回归分析，可以得到各个变量的膨胀系数VIF以及容忍度tolerance，如果容忍度越接近0，则共线性问题越严重，而VIF是越大共线性越严重，通常VIF小于5可以认为共线性不严重，宽泛一点的标准小于10即可。】

【因为深度学习不需要处理数据特征，自身可以学习】

共线性问题有如下几种检验方法：

相关性分析。检验变量之间的相关系数；

方差膨胀因子VIF。当VIF大于5或10时，代表模型存在严重的共线性问题；

条件数检验。当条件数大于100、1000时，代表模型存在严重的共线性问题

为什么不能将线性或逻辑回归模型的系数绝对值解释为特征重要性？

【因为很多现有线性回归量为每个系数返回P值，对于线性模型，许多实践者认为，系数绝对值越大，其对应特征越重要。事实很少如此，因为：

(a)改变变量尺度就会改变系数绝对值；

(b)如果特征是线性相关的，则系数可以从一个特征转移到另一个特征。此外，数据集特征越多，特征间越可能线性相关，用系数解释特征重要性就越不可靠。】

逻辑回归在训练的过程当中，如果有很多的特征高度相关或者说有一个特征重复了100遍，会造成怎样的影响？

结论：如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。原因：因为损失函数为凸函数，最终它会收敛到全局最小值，不再变化。因为LR是线性模型，其特征重复仅在每个特征分配权重缩小为百分之一，最后得到总结果和一个特征是一样的。】

为什么我们还是会在训练的过程当中将高度相关的特征去掉？

【形式简单，模型可解释性好。训练速度快。资源占用内存小】

LR如何防止过拟合：

【增加正则化项，L1、L2】

LR分布式训练怎么做

【LR的并行化最主要的就是对目标函数梯度计算的并行化。梯度计算就是向量的点乘和相加，可通过按行或按列切分样本数据并行计算梯度，最后合并结果】

LR如何解决线性不可分问题？或者问LR为何常常要做特征组合？

【逻辑回归本质上是一个线性模型，但是，这不意味着只有线性可分的数据能通过LR求解，实际上，我们可以通过2种方式帮助LR实现：（1）利用特殊核函数，对特征进行变换：把低维空间转换到高维空间，而在低维空间不可分的数据，到高维空间中线性可分的几率会高一些。（2）扩展LR算法，提出FM算法。】

LR为什么使用Sigmoid，

【数学上：因为LR服从伯努利分布，伯努利分布转化成广义线性模型指数分布族形式里可推导出sigmoid函数；概率上：sigmoid自身性质，值域在（0,1）之间，满足概率的要求】

LR为什么要对连续数值特征进行离散化？

【计算速度快，简单化模型，降低过拟合，可以做特征组合，对异常数据有强鲁棒性】

①离散特征的增加和减少都很容易，易于模型的快速迭代；

②稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；

③离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；

④逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；

⑤离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；

⑥特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

⑦特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

李沐曾经说过：模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

LR与SVM的联系与区别：

联系：

1、LR和SVM都可以处理分类问题，且一般都用于处理线性二分类问题（在改进的情况下可以处理多分类问题）

2、两个方法都可以增加不同的正则化项，如l1、l2等等。所以在很多实验中，两种算法的结果是很接近的。

区别：

1、LR是参数模型[逻辑回归是假设y服从Bernoulli分布]，SVM是非参数模型，LR对异常值更敏感。

2、从目标函数来看，区别在于逻辑回归采用的是logistical loss，SVM采用的是hinge loss，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。

3、SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。

4、逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些，SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。

5、logic 能做的 svm能做，但可能在准确率上有问题，svm能做的logic有的做不了。

如何选择LR与SVM？

非线性分类器，低维空间可能很多特征都跑到一起了，导致线性不可分。

①如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM

②如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel

③如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况。

模型复杂度：SVM支持核函数，可处理线性非线性问题;LR模型简单，训练速度快，适合处理线性问题;决策树容易过拟合，需要进行剪枝

损失函数：SVM hinge loss; LR L2正则化;

adaboost 指数损失数据敏感度：SVM添加容忍度对outlier不敏感，只关心支持向量，且需要先做归一化; LR对远点敏感

数据量：数据量大就用LR，数据量小且特征少就用SVM非线性核

什么是参数模型（LR）与非参数模型（SVM）？

在统计学中，参数模型通常假设总体（随机变量）服从某一个分布，该分布由一些参数确定（比如正太分布由均值和方差确定），在此基础上构建的模型称为参数模型；

非参数模型对于总体的分布不做任何假设，只是知道总体是一个随机变量，其分布是存在的（分布中也可能存在参数），但是无法知道其分布的形式，更不知道分布的相关参数，只有在给定一些样本的条件下，能够依据非参数统计的方法进行推断。

逻辑回归怎么多分类

【把Sigmoid函数换成softmax函数，即可适用于多分类的场景。】

softmax公式，为什么用sigmoid函数进行非线性映射（从二项分布的伯努利方程角度）

Logistic回归能处理浮点数吗？

一、理解RDD

二、RDD的生命周期

三、RDD依赖

四、RDD的基本操作

1、基本的RDD

（1）建立RDD

（2）转换操作

（3）动作操作

（4）通过pipe方法调用系统命令操作RDD

（5）mapPartitions：每次处理一个分区

（6）mapPartitionsWithIndex：接收两个参数，一个位分区的索引和另一个为 遍历分区内所有项的迭代器。

（7）foreachPartition：与mapPartitions函数类似，但不需要返回值

（8）glom: 将每个分区都转换为数组。

2. 键值对PairRDD：算子中包含ByKey的都是针对PairRDD

（1）创建PairRDD

(2) 转换操作

(3) 动作操作

五、代码学习

1. 建立RDD

2. RDD与Dataframe的转换

3. rdd函数

更好的解决方案：reduceByKey,非groupBykey

Spark生态架构图

Spark简介

1. 概念

2. 组件关系

3. 运行流程

（1）概念层级

Driver

Spark Context/Session

Cluster Manager

Executor

（2）代码层级

(3) spark中Master与Worker区别及Driver与Executor区别

4. DAGScheduler具体流程

5. MR和spark区别

（1）中间结果输出：

（2）数据格式：

（3）容错性：

（4）通用性：

（5）执行策略

6、spark1.x和spark2.x的区别

7. spark 应用执行模式

（1）local模式

（2）standalone：

（3）YARN

8. 提交任务方法

9. 参数配置：

过拟合

一、概念

正则化/惩罚项

一、概念

二、 从数学角度解释正则化为什么能提升模型的泛化能力；【奥卡姆剃刀：简单就好】

三、L1和L2范数各有什么特点以及相应的原因？L1和L2的区别与应用场景；

四、解释L1范数更容易产生稀疏的权重，L2不的原因：

（1）几何角度

（2）公式角度：（拉格朗日求导）

（3）贝叶斯先验

一、均值、方差、协方差

一、BN批标准化

1、BN的基本动机

2、 BN的原理

广告校准

1. 业务背景

2. 面临的问题

3. 校准算法

（1） Bias Correction：负采样率修正

（2）校准算法—保序回归

（3）校准算法3 —-SIR（保序回归平滑校准算法）

（4）校准算法4—贝叶斯平滑SIR校准算法（Bayes-SIR)

梯度下降

1. 重点

2. 概念

（1）常用的优化方法：直接法、迭代法（梯度下降、牛顿法、拟牛顿法、共轭梯度法）

（2）直接法（求解析解）：

（3）牛顿法：

（4） GD 梯度下降:

3. 梯度下降法和牛顿法的区别

4. 三种变形

（1）Batch gradient descend【批量梯度下降】

（6）mapPartitionsWithIndex：接收两个参数，一个位分区的索引和另一个为遍历分区内所有项的迭代器。

二、从数学角度解释正则化为什么能提升模型的泛化能力；【奥卡姆剃刀：简单就好】