类型一:树的深度
题目1:二叉树的最大深度
题目描述
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明 : 叶子节点是指没有子节点的节点。
示例 :
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
思路1:递归
边界: 一旦root == None则返回深度为0。否则进入递归子问题。
递归子问题: max(左树深度,右树深度)+ 1
代码1
1 | def dfs(root): |
思路2:深度遍历DFS
边界:一旦root == None则记录深度大小tmp,判断是否大于res(结果)。否则进入递归子问题。
递归子问题:将当前深度tmp+1,传入左子树和右子树
代码21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.left.right = TreeNode(5)
#全局变量
res = 0
def dfs(root,tmp):
global res
##边界
if not root:
res = max(res,tmp)
return
###递归子问题
else:
dfs(root.left,tmp+1)
dfs(root.right,tmp+1)
dfs(root,0)
print(res)
代码31
2
3
4
5
6
7
8
9
10
11res = 0
def dfs(root,height):
global res
if root:
if not root.left and not root.right:
self.res = max(res,height)
else:
dfs(root.left,height+1)
dfs(root.right,height+1)
dfs(root,1)
print(res)
题目2:二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
1 | 3 |
返回它的最小深度 2.
思路1:DFS
如果根节点没有左子树或右子树,则返回( 1+左子树深度+右子树深度)
如果根节点左右子树都有,则返回(1+min(左子树深度,右子树深度)
代码
1 | def minDepth(root) |
思路2:迭代
层次遍历,一旦有一层存在左右子树都没有,则返回height
1 | def minDepth(self, root): |
题目3:平衡二叉树
题目描述
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
1 | 3 |
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1 | 1 |
返回 false 。
思路:DFS
【和求深度思想一样】
代码
1 | # class TreeNode(object): |
题目4:找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:
1 | 输入: |
示例 2:
1 | 输入: |
思路1:DFS
维护一个最大深度 self.height 如果深度更新,则对应的值也更新。
这里注意先更新右边再更新左边,这样最后的值将会是最左边的值,左边的值会把右边的覆盖掉,如果深度相同的话
代码1
1 | def leftValue(root): |
思路2:层次遍历
代码2
1 | def leftValue(root): |
题目5:二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
1 | 输入: [1,2,3,null,5,null,4] |
思路1:DFS
代码11
2
3
4
5
6
7
8
9
10
11
12
13def treeRight(root):
if not root:
return []
res = [root.val]
def dfs(root,height):
if not root:
return
if len(res) < height:
res.append(root.val)
dfs(root.right,height+1)
dfs(root.left,height+1)
dfs(root,1)
return res
思路2:层次遍历
1 | def rightSideView(root): |
题目6:在每个树行中找最大值
您需要在二叉树的每一行中找到最大的值。
示例:
1 | 输入: |
思路1:层次遍历
代码11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def largestValues(root):
if not root:
return []
res = [root.val]
prev = [root]
while prev:
cur = []
while prev:
node = prev.pop()
if node.left:
cur.append(node.left)
if node.right:
cur.append(node.right)
if cur:
res.append(max([i.val for i in cur]))
prev = cur
return res
思路2:DFS
代码21
2
3
4
5
6
7
8
9
10
11
12
13
14def largestValues(root):
if not root:
return []
res = [root.val]
def dfs(root,height):
if root:
if len(res) <= height:
res.append(root.val)
if len(res) > height and root.val > res[height]:
res[height] = root.val
dfs(root.left,height + 1)
dfs(root.right,height+1)
dfs(root,0)
return res
类型二:树的路径
题目1:二叉树的所有路径
题目描述
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: [“1->2->5”, “1->3”]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
思路:DFS
边界:
如果root==None,不管
如果root.left和root.right同时为空,则将这条路径加入res数组中。
递归子问题:
如果root.left或者root.right有一个不为空,继续dfs(root.left,path),dfs(root.right,path)
代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Node():
def __init__(self,value):
self.val = value
self.left = None
self.right = None
def test(root):
if not root:
return []
res = []
def dfs(root,path):
if root:
path = path + str(root.val) + '->'
if not root.left and not root.right:
res.append(path[:-2])
else:
dfs(root.left,path)
dfs(root.right,path)
dfs(root,'')
return res
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
test(root)
题目2:路径总和
题目描述
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路:DFS
查看每条路径和是否等于sum,
递归边界:没有左子树也没有右子树时,判断是否等于sum。
递归子问题:递归左子树,递归右子树
代码
1 | def hasPathSum(root,sum): |
题目3:路径总和II
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
思路:DFS
1 | def pathSum(root,sum): |
题目4:叶子相似的树
题目描述
请考虑一颗二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

举个例子,如上图所示,给定一颗叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两颗二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
提示:
- 给定的两颗树可能会有
1到100个结点。
思路:DFS
思路和二叉树的所有路径一样,边界只有遇到叶子节点才将其加入res中。
代码:
1 | def leafsimilar(root1,root2): |
题目5:求根到叶子节点数字之和
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
1 | 输入: [1,2,3] |
示例 2:
1 | 输入: [4,9,0,5,1] |
思路:DFS
代码
1 | def sumNumbers(self, root: TreeNode) -> int: |
题目6:节点与其祖先之间的最大差值
给定二叉树的根节点 root,找出存在于不同节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例:
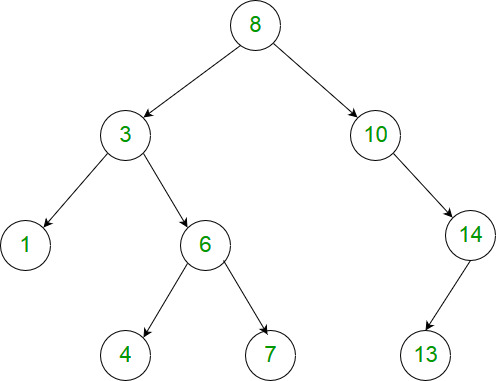
1 | 输入:[8,3,10,1,6,null,14,null,null,4,7,13] |
思路:DFS
找树的每条路径中的最小值和最大值。
代码
1 | class Solution: |
类型三:二叉树类型
题目1:对称二叉树
题目描述
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 | 1 |
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1 | 1 |
思路1:DFS
先判断二叉树是否是平衡树,
比如有两个节点left, right,
需要比较left的左子节点的值和right的右子节点的值是否相等,
同时还要比较left的右子节点的值和right的左子结点的值是否相等,
以此类推比较完所有的左右两个节点。
代码1
1 | def isSymmetric(root): |
思路2:迭代
层次遍历,判断每层数据是否是对称的。
代码2
1 | def isSymmetric(root): |
类型四:二叉树操作
题目1:在二叉树中分配硬币
给定一个有 N 个结点的二叉树的根结点 root,树中的每个结点上都对应有 node.val 枚硬币,并且总共有 N 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点,或者从子结点移动到父结点。)。
返回使每个结点上只有一枚硬币所需的移动次数。
示例 1:
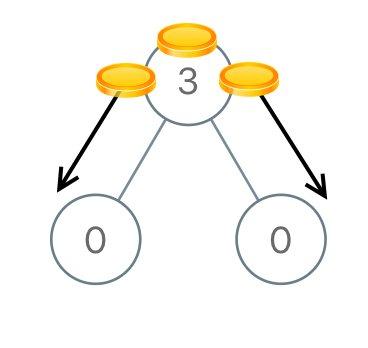
1 | 输入:[3,0,0] |
示例 2:
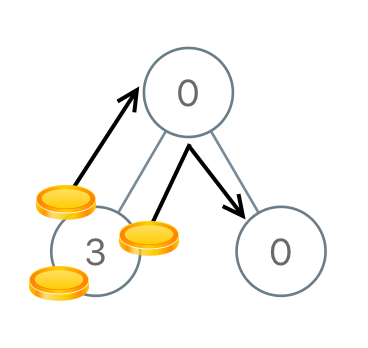
1 | 输入:[0,3,0] |
示例 3:
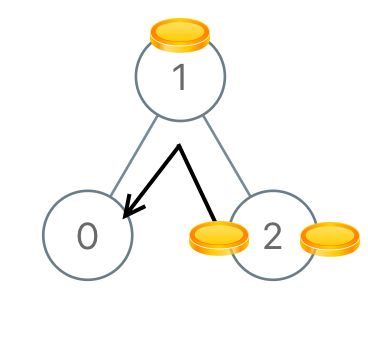
1 | 输入:[1,0,2] |
示例 4:
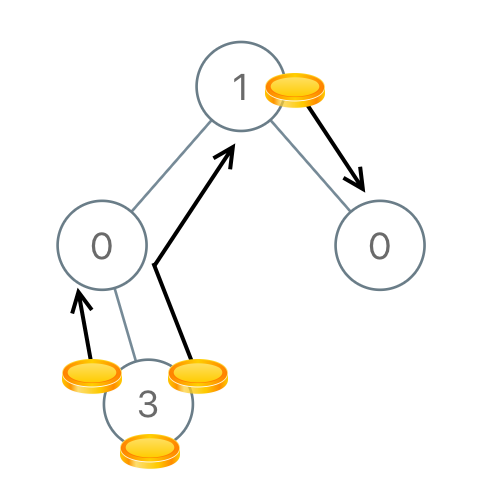
1 | 输入:[1,0,0,null,3] |
提示:
1<= N <= 1000 <= node.val <= N
思路:DFS

代码:
1 | class Solution: |