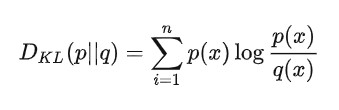本篇博客仅作为学习,如有侵权必删。
[TOC]
逻辑回归
1. LR重点
LR的重点:
- 目的:LR解决二分类问题。
- 输出结果:(0,1)之间的数值。
- 模型:线性模型 + sigmoid函数
- y_pred = sigmoid(W0+W1 x1 + … + Wn xn) = sigmoid(∑W^TX)
- LR为何用sigmoid函数? sigmoid的性质
- 损失函数:loss = -(∑y) log y_pred_i + (1-yi) log(1 - y_pred_i))
- 损失函数的推导:
- 求解方法:梯度下降
2. 概念
二分类:假设有一批训练样本集合X={x1,x2,…,xn},其中xi有a个属性,对这些样本分类属于0还是1?
伯努利分布:离散型概率分布,成功则随机变量取值为1,失败则为0,设置成功的概率为p,则失败的概率为1-p,N次实验后,成功期望是Np,方差为 Np(1-p)
期望/均值:实验中每次可能结果的概率乘其结果的总和。E(X)=∑xP(X), x表示随机变量的取值,P(X)表示随机变量X=x的概率。
方差:概率分布的数据期望,反映了随机变量取值的变异程度。D(x ) = E{[X-E(X)]^2}=E(X^2) - [ E(X)]^2
似然函数(联合概率密度函数):
先验概率:根据以往经验和分析得到的概率。主观上的经验估计p(x)
似然函数:在给定参数θ情况下得到结果 X 的概率分布p(x|θ) 。
(给定输出x时,使得函数得到X概率最大的关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率, 即L(θ|x) = P(X=x|θ))
后验概率:在给定结果信息X的情况下得到参数 θ 的概率: p(θ|x) 。
梯度下降:一种求解模型的方法,后面细看。
LR:假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,达到将数据二分类的目的。
3. LR模型和损失函数
模型和损失函数得到的过程:
第①步:引入参数θ=(θ1,θ2……),对于样本加权θ^TX
第②步:引入logit函数:g(z)=1/(1+e^-z),令z=θ^TX,故LR的模型:
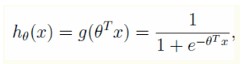
假设样本服从的是伯努利分布(0-1分布):
以上h的含义是:表示样本x属于类别1的概率,即P(y=1|x;θ)。则样本x属于类别0的概率为1-hθ(x)。
联合两个概率即为似然函数。
第③步:似然函数(联合概率密度函数):

所有样本的似然函数:(令概率最大化)
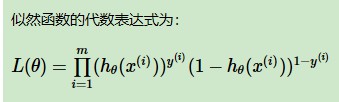
第④步:损失函数(对数似然函数取反min):交叉熵损失函数
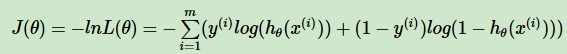
4. 损失函数的来源推导
法一:假设服从伯努利分布,伯努利分布的极大似然估计
- 假设样本服从伯努利(0-1)分布,有:
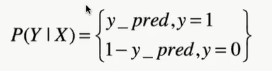
法二:熵角度确定损失函数
KL散度(相对熵):KL散度可以用来
衡量两个分布之间的差异程度。若两者差异越小,KL散度越小,反之亦反。当两分布一致时,其KL散度为0。 相关概念请看:熵的章节
如果是两个随机变量P,Q,且其概率分布分别为p(x),q(x),则p相对q的相对熵为:
模型预估值分布和实际值分布的KL散度:(KL散度越小,表明两个分布越相似,即预估值越接近实际值)。
p log(p/q) = p logp - p* logq
其中, p logp是一个定值(实际值分布p = y_i,是固定的,0或1),- p logq是交叉熵,只要交叉熵较大,则KL散度就越小,预测值和实际值越相似。
交叉熵:令-p log q = -y_i log y_pred_i . (可扩展为多个: -(y1 log y_pred_1 + y2 log y_pred_2 + y3 * log y_pred_3.。。。)
法三、贝叶斯学派确定损失函数
贝叶斯公式:
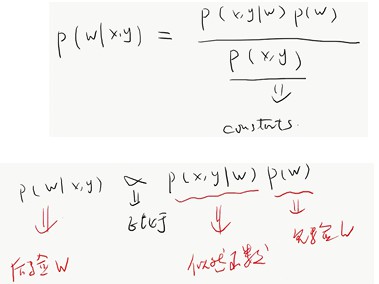
贝叶斯学派有先验函数,频率学派仅考虑似然函数。
贝叶斯用上一次的后验当成下一次的先验与似然函数相乘,计算下一次的后验,不断迭代。
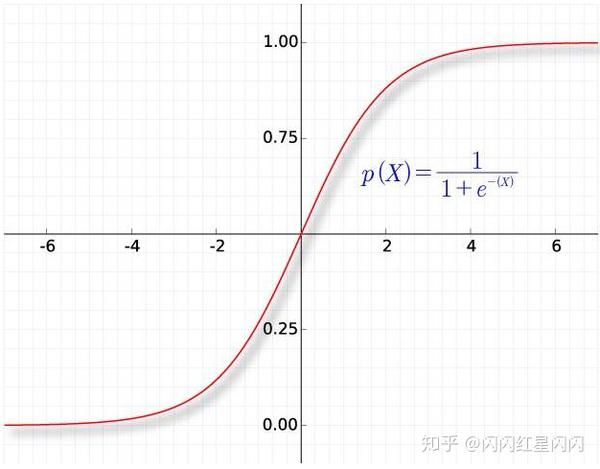
5. LR为何用sigmoid函数?
(1)数学上
1. 因为LR服从伯努利分布,伯努利分布转化为广义线性模型指数分布族形式里可推导出sigmoid函数
(2)概率上:
sigmoid自身性质,值域在(0,1)之间,满足概率的要求
(3)单调性:
若sigmoid不具备单调性,LR不可用其作为映射函数。
下图的g1 < g2的x指的是线性中的g=wx的值。若LR的映射函数不具备单调性,则同一个y值会对应两个g值。
因为x是给定的特征,则w没办法学习,因为LR是个记忆函数,在g1之前当学习w发现增大w1能让y接近高点(即在g1和g2之间)时,突然发现当w1更大时(大于g2),y越来越小,没办法沿着某些方向学习w值。
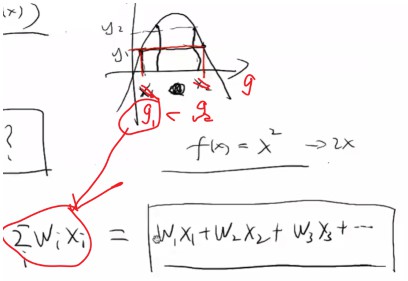
- sigmoid具备单调性,则在使用redis存储参数w的key和value时,若推荐最终结果只涉及排序,则无需进行sigmoid计算,且若是离散特征,只需将x特征值为1对应的参数w相加得到最终值进行排序即可。又可以提高效率了。
sigmoid性质:
- 定义域:(-∞,+∞)
- 将任意input压缩到(0,1)之间,即值域为(0,1),符合概率定义
- 设f(x) = sigmoid(x), f(x)导数为f(x)*(1-f(x)), 对梯度下降有好处,前向传递时计算结果可以保留,BP时可以直接用来计算,加快速度
- 1/2处导数最大, 两边梯度趋于饱和,容易发生梯度消失(作为激活函数的弊端)
- 不以原点为中心,BP时梯度下降更新慢,更新时以zigzag(折线)方式更新。(作为激活函数的弊端)
- 单调性,LR的映射函数如果没有单调性不行。
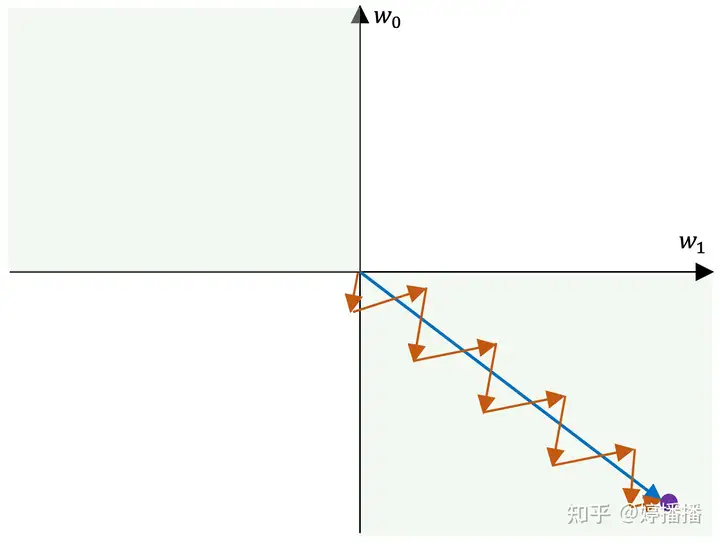
6.【为什么参数的梯度方向一致容易造成zigzag现象】
当所有梯度同为正或者负时,参数在梯度更新时容易出现zigzag现象。
zigzag现象如图4所示,不妨假设一共两个参数, w0 和 w1 ,紫色点为参数的最优解,蓝色箭头表示梯度最优方向,红色箭头表示实际梯度更新方向。
由于参数的梯度方向一致,要么同正,要么同负,因此更新方向只能为第三象限角度或第一象限角度,而梯度的最优方向为第四象限角度,也就是参数 w0 要向着变小的方向, w1 要向着变大的方向,在这种情况下,每更新一次梯度,不管是同时变小(第三象限角度)还是同时变大(第四象限角度),总是一个参数更接近最优状态,另一个参数远离最优状态,因此为了使参数尽快收敛到最优状态,出现交替向最优状态更新的现象,也就是zigzag现象。
7. 梯度下降求解损失函数
梯度下降概念:根据loss求导,往


注意:这里梯度更新时用加号是因为max loss。 非min loss的值。
8. LR的优缺点
优点:
- 1、形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大。
- 2、模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差,并且特征工程可以大家并行开发,大大加快开发的速度。
- 3、训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
- 4、资源占用小,尤其是内存。因为只需要存储各个维度的特征值。
- 5、方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)。
- 6、对稀疏数据比较友好。一个特征通过 one-hot : [0,0,1,……,0] ,LR是个记忆模型,将该特征扔进LR之后,会将x3=1(w3)记得很好,别的都为0了,但这样也容易过拟合。(gbm,深度模型这些都不太喜欢稀疏数据)
缺点:
- 准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
- 很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。
- 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。
- 逻辑回归本身无法筛选特征。有时候,我们会用gbdt来筛选特征,然后再上逻辑回归。
- 对模型中自变量多重共线性较为敏感,例如两个高度相关自变量同时放入模型,可能导致较弱的一个自变量回归符号不符合预期,符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量,以减少候选变量之间的相关性;
- 必须对缺失值处理
9. 扩展问题
- 线性回归与LR的本质区别:
【线形回归与 逻辑回归的本质区别是前者用于回归后者用于分类,二者都是线形模型。】
什么情况下用LR【大规模样本下的线性二分类】
LR的损失函数的公式和函数
逻辑回归的损失函数为什么要使用极大似然函数作为损失函数?
【如果激活函数为sigmoid函数,使用均方误差作为损失函数的话为非凸函数,而使用对数损失函数为凸函数】
【损失函数一般有四种,平方损失函数、对数损失函数、铰链损失函数和绝对值损失函数。极大似然取对数之后相当于对数损失,在LR模型下,对数损失函数的训练求解参数速度是比较快的,不选平方损失函数是因为梯度更新的速度和sigmoid函数本身的梯度是相关的,这样训练会比较慢】
LR的推导过程
LR如何解决共线性,为什么深度学习不强调
【法1:岭回归(L2正则化)、
法2:主成分分析,
法3:共线性诊断常用的统计量:将所有回归中要用到的变量依次作为因变量、其他变量作为自变量进行回归分析,可以得到各个变量的膨胀系数VIF以及容忍度tolerance,如果容忍度越接近0,则共线性问题越严重,而VIF是越大共线性越严重,通常VIF小于5可以认为共线性不严重,宽泛一点的标准小于10即可。 】
【因为深度学习不需要处理数据特征,自身可以学习】
共线性问题有如下几种检验方法:
- 相关性分析。检验变量之间的相关系数;
- 方差膨胀因子VIF。当VIF大于5或10时,代表模型存在严重的共线性问题;
- 条件数检验。当条件数大于100、1000时,代表模型存在严重的共线性问题
为什么不能将线性或逻辑回归模型的系数绝对值解释为特征重要性?
【因为很多现有线性回归量为每个系数返回P值,对于线性模型,许多实践者认为,系数绝对值越大,其对应特征越重要。事实很少如此,因为:
(a)改变变量尺度就会改变系数绝对值;
(b)如果特征是线性相关的,则系数可以从一个特征转移到另一个特征。此外,数据集特征越多,特征间越可能线性相关,用系数解释特征重要性就越不可靠。】
逻辑回归在训练的过程当中,如果有很多的特征高度相关或者说有一个特征重复了100遍,会造成怎样的影响?
结论:如果在损失函数最终收敛的情况下,其实就算有很多特征高度相关也不会影响分类器的效果。原因:因为损失函数为凸函数,最终它会收敛到全局最小值,不再变化。因为LR是线性模型,其特征重复仅在每个特征分配权重缩小为百分之一,最后得到总结果和一个特征是一样的。】
为什么我们还是会在训练的过程当中将高度相关的特征去掉?
【形式简单,模型可解释性好。训练速度快。资源占用内存小】
LR如何防止过拟合:
【增加正则化项,L1、L2】
LR分布式训练怎么做
【LR的并行化最主要的就是对目标函数梯度计算的并行化。梯度计算就是向量的点乘和相加,可通过按行或按列切分样本数据并行计算梯度,最后合并结果】
LR如何解决线性不可分问题?或者问LR为何常常要做特征组合?
【逻辑回归本质上是一个线性模型,但是,这不意味着只有线性可分的数据能通过LR求解,实际上,我们可以通过2种方式帮助LR实现:(1)利用特殊核函数,对特征进行变换:把低维空间转换到高维空间,而在低维空间不可分的数据,到高维空间中线性可分的几率会高一些。(2)扩展LR算法,提出FM算法。】
LR为什么使用Sigmoid,
【数学上:因为LR服从伯努利分布,伯努利分布转化成广义线性模型指数分布族形式里可推导出sigmoid函数;概率上:sigmoid自身性质,值域在(0,1)之间,满足概率的要求】
LR为什么要对连续数值特征进行离散化?
【计算速度快,简单化模型,降低过拟合,可以做特征组合,对异常数据有强鲁棒性】
①离散特征的增加和减少都很容易,易于模型的快速迭代;
②稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
③离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
④逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合;
⑤离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
⑥特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
⑦特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
李沐曾经说过:模型是使用离散特征还是连续特征,其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型,也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说,前者容易,而且可以n个人一起并行做,有成功经验;后者目前看很赞,能走多远还须拭目以待。
LR与SVM的联系与区别:
联系:
1、LR和SVM都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题)
2、两个方法都可以增加不同的正则化项,如l1、l2等等。所以在很多实验中,两种算法的结果是很接近的。
区别:
1、LR是参数模型[逻辑回归是假设y服从Bernoulli分布],SVM是非参数模型,LR对异常值更敏感。
2、从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
3、SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
4、逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
5、logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
如何选择LR与SVM?
非线性分类器,低维空间可能很多特征都跑到一起了,导致线性不可分。
①如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
②如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
③如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况。
模型复杂度:SVM支持核函数,可处理线性非线性问题;LR模型简单,训练速度快,适合处理线性问题;决策树容易过拟合,需要进行剪枝
损失函数:SVM hinge loss; LR L2正则化;
adaboost 指数损失数据敏感度:SVM添加容忍度对outlier不敏感,只关心支持向量,且需要先做归一化; LR对远点敏感
数据量:数据量大就用LR,数据量小且特征少就用SVM非线性核
什么是参数模型(LR)与非参数模型(SVM)?
在统计学中,参数模型通常假设总体(随机变量)服从某一个分布,该分布由一些参数确定(比如正太分布由均值和方差确定),在此基础上构建的模型称为参数模型;
非参数模型对于总体的分布不做任何假设,只是知道总体是一个随机变量,其分布是存在的(分布中也可能存在参数),但是无法知道其分布的形式,更不知道分布的相关参数,只有在给定一些样本的条件下,能够依据非参数统计的方法进行推断。
逻辑回归怎么多分类
【把Sigmoid函数换成softmax函数,即可适用于多分类的场景。】
softmax公式,为什么用sigmoid函数进行非线性映射(从二项分布的伯努利方程角度)
Logistic回归能处理浮点数吗?